Question

8．三棱锥P-ABC中，
（1）若点P到AB，BC，CA的距离相等，那么点P在底面内的射影是△ABC的内心或旁心；
（2）若两组对棱互相垂直，那么点P在底面内的射影是△ABC的垂心．

Answer 1

分析 （1）根据题意得出点P在平面ABC内的射影到三边的距离相等，是内心或旁心；
（2）根据题意得出点P在底面ABC内的射影O是△ABC的垂心．

解答 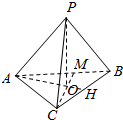解：三棱锥P-ABC中，
（1）点P到AB，BC，CA的距离相等，则点P在平面ABC内的射影到三边的距离也相等，
到三角形三边距离相等的点是三角形的内心或是旁心，
所以点P在底面的射影是△ABC的内心或旁心；
（2）若两组对棱互相垂直，如图所示，
PA⊥BC，PC⊥AD，
容易得出AH⊥BC，CM⊥AB，
所以点P在底面ABC内的射影O是△ABC的垂心．
故答案为：（1）内心或旁；（2）垂．

点评 本题考查了三角形五心的概念及线线垂直判断问题，因为旁心和内心都符合到三角形三边距离相等的条件，我们的教学中只注重内心问题，是综合题目．