练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
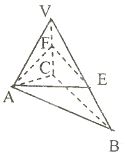
    如图所示，侧棱长为2
    		3
    的正三棱锥V-ABC中，∠AVB=∠BVC=∠CVA=30°，过A作截面AEF，则截面三角形AEF周长的最小值是
    2
    		6
    2
    		6
    ．
    分析：根据题意，将正三棱锥V-ABC沿着侧棱VA展开在同一个平面内，如图所示，可得图中的AA'长即为截面△AEF周长的最小值，再根据题中数据利用勾股定理即可算出这个最小值．
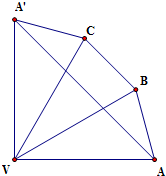    解答：解：如图所示，沿着侧棱VA把正三棱锥V-ABC展开在同一个平面内，
    可得图中的AA'的长即为截面△AEF周长的最小值，
    ∵∠AVB=∠BVC=∠CVA=30°，
    ∴∠AVA′=3×30=90°．
    Rt△VAA′中，由勾股定理可得
    AA'=
    		VA2+VA′2
    =
    		(2
    		3
    )2+(2
    		3
    )    2
    =2
    		6
    ，
    故答案为：2
    		6
    点评：本题给出正三棱锥，求截面三角形AEF周长的最小值．着重考查了正三棱锥的性质、锥体的平面展开图和勾股定理等知识，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示,正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为,若经过对角线AB1且与对角线BC1平行的平面交上底面一边A1C1于点D.

    (1)确定点D的位置,并证明你的结论;

    (2)求二面角A1 –AB-1D的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示的一组图形为某一四棱锥S—ABCD的侧面与底面，

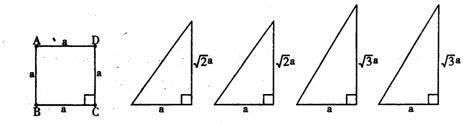
    (1)指出各侧棱长；

    （2）在（1）的条件下，过A且垂直于SC的平面分别交于SB、SC、SD于E、F、G.

    求（1）（2）的条件下，求二面角A—SC—B的大小.

    查看答案和解析>>

    科目：高中数学 来源：2015届安徽合肥一中高二上学期第一次月考理科数学试卷（解析版） 题型：解答题

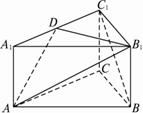
    如图所示，四棱柱ABCD－A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA1＝AB＝2，E为棱AA1的中点．

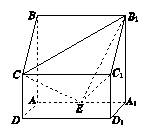
    (1)证明：B1C1⊥CE；

    (2)设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为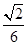.求线段AM的长．

     

    查看答案和解析>>

    科目：高中数学 来源：上海市模拟题 题型：解答题

    如图所示, 直四棱柱的侧棱长为, 底面是边长, 的矩形,为的中点,
    (1)求证: 平面；
    (2)求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC的中点,它的正(主)视图和侧(左)视图如图所示.

    (1)证明:AD⊥平面PBC.

    (2)求三棱锥D-ABC的体积.

    (3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.

    查看答案和解析>>

    同步练习册答案