
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右准线方程
的右准线方程![]() ,离心率
,离心率![]() ,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
,左、右顶点分别为A,B,右焦点为F,点P在椭圆上,且位于x轴上方.
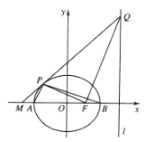
(Ⅰ)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)点Q在右准线l上,且![]() ,直线
,直线![]() 交x负半轴于点M,若
交x负半轴于点M,若![]() ,求点P坐标.
,求点P坐标.
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 先把高二年级的2000名学生编号为1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() 的学生,这样的抽样方法是系统抽样法;
的学生,这样的抽样方法是系统抽样法;
B. 独立性检验中,![]() 越大,则越有把握说两个变量有关;
越大,则越有把握说两个变量有关;
C. 若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
D. 若一组数据1、a、3的平均数是2,则该组数据的方差是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县位于沙漠地带,人与自然长期进行顽强的斗争,到1996年底全县的绿化率已达到30%(成为绿洲).从1997年开始,每年将出现这样的局面,原有沙漠面积的16%被栽上树,改造为绿洲,而同时,原有绿洲面积的4%又被侵蚀,变为沙漠.
(1)设全县面积为1,1996年底绿洲面积为![]() ,经过
,经过![]() 年绿洲面积为
年绿洲面积为![]() .求证:
.求证:![]() .
.
(2)至少需经过多少年的努力才能使全县的绿化率超过60%(年取整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
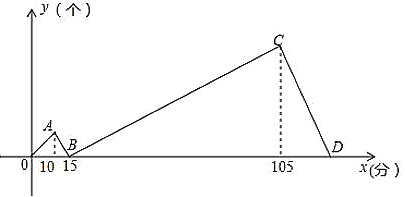
【题目】甲乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为10,B点坐标为![]() ,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提升城市道路通行能力,可为市民提供更多出行便利.我校某研究性学习小组对成都市一中心路段(限行速度为![]() 千米/小时)的拥堵情况进行调查统计,通过数据分析发现:该路段的车流速度
千米/小时)的拥堵情况进行调查统计,通过数据分析发现:该路段的车流速度![]() (辆/千米)与车流密度
(辆/千米)与车流密度![]() (千米/小时)之间存在如下关系:如果车流密度不超过
(千米/小时)之间存在如下关系:如果车流密度不超过![]() 该路段畅通无阻(车流速度为限行速度);当车流密度在
该路段畅通无阻(车流速度为限行速度);当车流密度在![]() 时,车流速度是车流密度的一次函数;车流密度一旦达到
时,车流速度是车流密度的一次函数;车流密度一旦达到![]() 该路段交通完全瘫痪(车流速度为零).
该路段交通完全瘫痪(车流速度为零).
(1)求![]() 关于
关于![]() 的函数
的函数![]()
(2)已知车流量(单位时间内通过的车辆数)等于车流密度与车流速度的乘积,求此路段车流量的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某便利店每天以每件5元的价格购进若干鲜奶,然后以每件10元价格出售,如果当天卖不完,剩下的鲜奶作餐厨垃圾处理.便利店记录了100天这种鲜奶的日需求量![]() (单位:件)如表所示:
(单位:件)如表所示:
日需求量n(件) | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
频数 | 10 | 20 | 16 | 16 | 15 | 12 | 11 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若便利店一天购进160件这种鲜奶,X表示当天的利润(单位:元),求X的分布列与数学期望及方差;
(2)若便利店一天购进160件或170件这种鲜奶,仅从获得利润大的角度考虑,你认为应购进160件还是170件?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com