
如图,在长方体 ,中,
,中, ,点
,点 在棱AB上移动.
在棱AB上移动.

(Ⅰ)证明: ;
;
(Ⅱ)当 为
为 的中点时,求点
的中点时,求点 到面
到面 的距离;
的距离;
(Ⅲ) 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.
(Ⅰ)详见解析;(Ⅱ)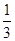 ;(Ⅲ)
;(Ⅲ)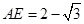 .
.
【解析】
试题分析:(Ⅰ)建立空间坐标,分别求出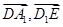 的坐标,利用数量积等于零即可;(Ⅱ)当
的坐标,利用数量积等于零即可;(Ⅱ)当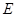 为
为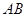 的中点时,求点
的中点时,求点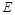 到平面
到平面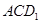 的距离,只需找平面
的距离,只需找平面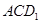 的一条过
的一条过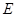 点的斜线段
点的斜线段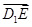 在平面
在平面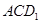 的法向量上的投影即可;(Ⅲ)设
的法向量上的投影即可;(Ⅲ)设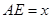 ,因为平面
,因为平面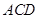 的一个法向量为
的一个法向量为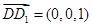 ,只需求出平面
,只需求出平面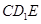 的法向量,然后利用二面角为
的法向量,然后利用二面角为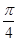 ,根据夹角公式,求出
,根据夹角公式,求出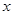 即可.
即可.
试题解析:以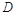 为坐标原点,直线
为坐标原点,直线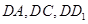 分别为
分别为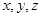 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设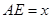 ,则
,则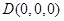 ,
,
(Ⅰ)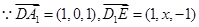 ,
,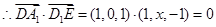 ,故
,故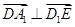 ;
;
(Ⅱ)因为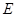 为
为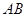 的中点,则
的中点,则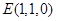 ,从而
,从而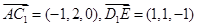 ,
, 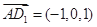 ,设平面
,设平面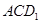 的法向量为
的法向量为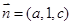 ,则
,则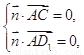 也即
也即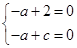 ,得
,得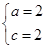 ,从而
,从而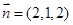 ,所以点
,所以点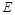 到平面
到平面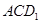 的距离为
的距离为
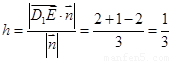 ;
;
(Ⅲ)设平面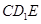 的法向量
的法向量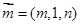 , 而
, 而 , 由
, 由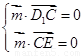 ,即
,即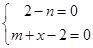 ,得
,得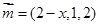 ,依题意得:
,依题意得: 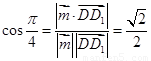 ,
,
 ,解得
,解得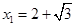 (不合,舍去),
(不合,舍去),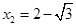 ∴
∴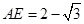 时,二面角
时,二面角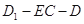 的大小为
的大小为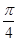 .
.
考点:空间向量在立体几何中应用.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
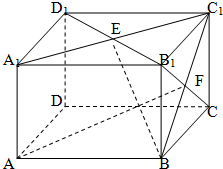 如图,在长方体AC1中,AB=BC=2,AA1=
如图,在长方体AC1中,AB=BC=2,AA1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
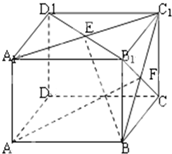 如图,在长方体AC中,AB=BC=2,AA1=
如图,在长方体AC中,AB=BC=2,AA1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
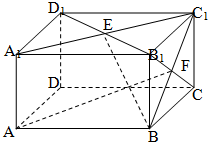 如图,在长方体AC1中,AB=BC=2,AA1=
如图,在长方体AC1中,AB=BC=2,AA1=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com