.(本小题满分12分)
已知向量
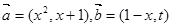
,若函数
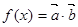
在区间
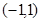
上是增函数,求
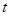
的取值范围。
解:由题意知:
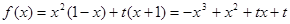
,则
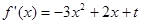
∵
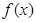
在区间
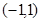
上是增函数,∴
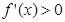
即
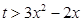
在区间
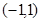
上是恒成立,
设
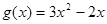
,则
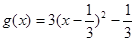
,于是有
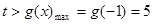
∴当
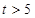
时,
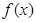
在区间
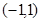
上是增函数
又当
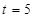
时,
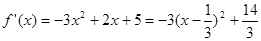
,
在
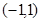
上,有
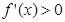
,即
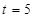
时,
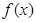
在区间
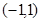
上是增函数
当
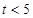
时,显然
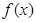
在区间
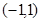
上不是增函数
∴
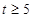
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
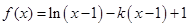
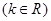
.
(1)若
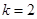
,求以
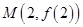
为切点的曲线的切线方程;
(2)若函数
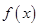
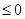
恒成立,确定实数K的取值范围;
(3)证明:
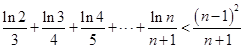
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
f(
x)为可导函数,且满足
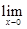

=-1,则过曲线
y=
f(
x)上点(1,
f(1))处的切线斜率为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
物体的运动方程是s = -
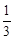
t
3+2t
2-5,则物体在t = 3时的瞬时速度为_
_ _.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知定义在
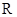
上的函数
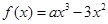
,其中
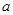
为大于零的常数.
(Ⅰ)当
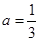
时,令
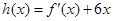
,求证:当
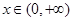
时,
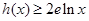
(
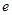
为自然对数的底数);
(Ⅱ)若函数
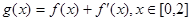
,在
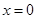
处取得最大值,求
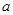
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
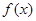
,当自变量由
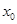
变化到
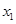
时函数值的增量与相应的自变量的增量比是函数
A.在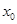 处的变化率 处的变化率 | B.在区间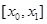 上的平均变化率 上的平均变化率 |
C.在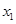 处的变化率 处的变化率 | D.以上结论都不对 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
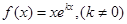
1.讨论函数
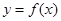
的单调性
2. 设
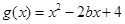
,当k=1时,若对于任意
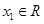
,存在
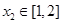
使得
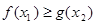
,求实数b的取值范围
查看答案和解析>>

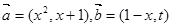 ,若函数
,若函数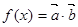 在区间
在区间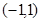 上是增函数,求
上是增函数,求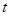 的取值范围。
的取值范围。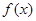 ,当自变量由
,当自变量由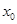 变化到
变化到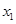 时函数值的增量与相应的自变量的增量比是函数
时函数值的增量与相应的自变量的增量比是函数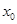 处的变化率
处的变化率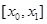 上的平均变化率
上的平均变化率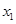 处的变化率
处的变化率