
【题目】对于定义域为R的函数f(x),若f(x)在(-∞,0)和(0,+∞)上均有零点,则称函数f(x)为“含界点函数”,则下列四个函数中,不是“含界点函数”的是( )
A. f(x)=x2+bx-1(b∈R) B. f(x)=2-|x-1|
C. f(x)=2x-x2 D. f(x)=x-sin x
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅱ)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 内存在两个极值点?若存在,求实数
内存在两个极值点?若存在,求实数![]() 的取值范围;若不存在,请说明理由. (参考数据:
的取值范围;若不存在,请说明理由. (参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
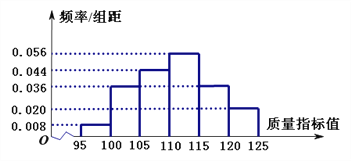
(Ⅰ)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(Ⅱ)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(Ⅲ)根据表1和图1,对两套设备的优劣进行比较.
附:

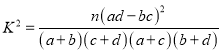 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE.求直线BC与平面ABF所成角的大小,并求线段PH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)当a<0时,讨论f(x)的单调性;
(2)若对任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=![]() ,n=
,n=![]() ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有___________________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,已知点![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
: ![]() 上的一点,斜率为
上的一点,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com