
分析 (1)由题意可求f(-$\frac{π}{2}$)=f(π)=sinπ=0,f(-$\frac{π}{4}$)=f($\frac{3π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$.
(2)设-$\frac{π}{2}≤x<\frac{π}{4}$,则$\frac{π}{4}<\frac{π}{2}-x≤π$,由f(x)=f($\frac{π}{2}-x$)=sin($\frac{π}{2}-x$)=cosx,即可解得分段函数的解析式f(x)=$\left\{\begin{array}{l}{sinx}&{x∈[\frac{π}{4},π]}\\{cosx}&{x∈[-\frac{π}{2},\frac{π}{4})}\end{array}\right.$.
(3)作函数f(x)的图象,若f(x)=a有解,则a∈[0,1],分情况讨论即可得解.
解答 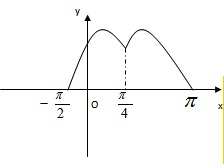 解:(1)f(-$\frac{π}{2}$)=f(π)=sinπ=0,
解:(1)f(-$\frac{π}{2}$)=f(π)=sinπ=0,
f(-$\frac{π}{4}$)=f($\frac{3π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$…3分
(2)设-$\frac{π}{2}≤x<\frac{π}{4}$,则$\frac{π}{4}<\frac{π}{2}-x≤π$,
∴f(x)=f($\frac{π}{2}-x$)=sin($\frac{π}{2}-x$)=cosx,
∴f(x)=$\left\{\begin{array}{l}{sinx}&{x∈[\frac{π}{4},π]}\\{cosx}&{x∈[-\frac{π}{2},\frac{π}{4})}\end{array}\right.$…6分
(3)作函数f(x)的图象如下:
显然,若f(x)=a有解,则a∈[0,1].
①若0$≤a<\frac{\sqrt{2}}{2}$,f(x)=a有两解,Ma=$\frac{π}{2}$;
②若a=$\frac{\sqrt{2}}{2}$,f(x)=a有三解,Ma=$\frac{3π}{4}$;
③若$\frac{\sqrt{2}}{2}$<a<1,f(x)=a有四解,Ma=π;
④若a=1,f(x)=a有两解,Ma=$\frac{π}{2}$;
综上所述,当0≤a<$\frac{\sqrt{2}}{2}$或a=1时,f(x)=a有两解,Ma=$\frac{π}{2}$;
当a=$\frac{\sqrt{2}}{2}$时,f(x)=a有三解,Ma=$\frac{3π}{4}$;
当$\frac{\sqrt{2}}{2}<a<1$时,f(x)=a有四解,Ma=π…12分
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了函数的对称性及应用,考查了数形结合思想和分类讨论思想的应用,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,3) | C. | (0,log23) | D. | (1,log23) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{\frac{1}{x^2}}$ | B. | $y=\frac{{{{({x-1})}^0}}}{x}$ | C. | $\frac{x+1}{{x({x+1})}}$ | D. | $y=\frac{{{x^2}+1}}{{x({{x^2}+1})}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com