
【题目】已知函数f(x)=aex(a≠0),g(x)=x2(Ⅰ)若曲线c1:y=f(x)与曲线c2:y=g(x)存在公切线,求a最大值.
(Ⅱ)当a=1时,F(x)=f(x)﹣bg(x)﹣cx﹣1,且F(2)=0,若F(x)在(0,2)内有零点,求实数b的取值范围.
【答案】解:(Ⅰ)设公切线l与c1切于点(x1 , a ![]() )与c2切于点(x2 ,
)与c2切于点(x2 , ![]() ), ∵f′(x)=aex , g′(x)=2x,
), ∵f′(x)=aex , g′(x)=2x,
∴ 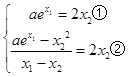 ,由①知x2≠0,
,由①知x2≠0,
①代入②得: ![]() =2x2 , 即x2=2x1﹣2,
=2x2 , 即x2=2x1﹣2,
由①知a= ![]() ,
,
设g(x)= ![]() ,g′(x)=
,g′(x)= ![]() ,
,
令g′(x)=0,得x=2;当x<2时g′(x)>0,g(x)递增.
当x>2时,g′(x)<0,g(x)递减.
∴x=2时,g(x)max=g(2)= ![]() ,∴amax=
,∴amax= ![]() .
.
(Ⅱ)F(x)=f(x)﹣bg(x)﹣cx﹣1=ex﹣bx2﹣cx﹣1,
∵F(2)=0=F(0),又F(x)在(0,2)内有零点,
∴F(x)在(0,2)至少有两个极值点,
即F′(x)=ex﹣2bx﹣c在(0,2)内至少有两个零点.
∵F″(x)=ex﹣2b,F(2)=e2﹣4b﹣2c﹣1=0,c= ![]() ,
,
①当b≤ ![]() 时,在(0,2)上,ex>e0=1≥2b,F″(x)>0,
时,在(0,2)上,ex>e0=1≥2b,F″(x)>0,
∴F″(x)在(0,2)上单调增,F′(x)没有两个零点.
②当b≥ ![]() 时,在(0,2)上,ex<e2≤2b,∴F″(x)<0,
时,在(0,2)上,ex<e2≤2b,∴F″(x)<0,
∴F″(x)在(0,2)上单调减,F′(x)没有两个零点;
③当 ![]() <b<
<b< ![]() 时,令F″(x)=0,得x=ln2b,
时,令F″(x)=0,得x=ln2b,
因当x>ln2b时,F″(x)>0,x<ln2b时,F″(x)<0,
∴F″(x)在(0,ln2b)递减,(ln2b,2)递增,
所以x=ln2b时,∴F′(x)最小=F′(ln2b)=4b﹣2bln2b﹣ ![]() +
+ ![]() ,
,
设G(b)=F′(ln2b)=4b﹣2bln2b﹣ ![]() +
+ ![]() ,
,
令G′(b)=2﹣2ln2b=0,
得2b=e,即b= ![]() ,当b<
,当b< ![]() 时G′(b)>0;当b>
时G′(b)>0;当b> ![]() 时,G′(b)<0,
时,G′(b)<0,
当b= ![]() 时,G(b)最大=G(
时,G(b)最大=G( ![]() )=e+
)=e+ ![]() ﹣
﹣ ![]() <0,
<0,
∴G(b)=f′(ln2b)<0恒成立,
因F′(x)=ex﹣2bx﹣c在(0,2)内有两个零点,
∴ 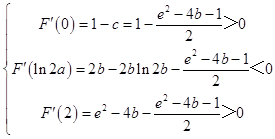 ,
,
解得: ![]() <b<
<b< ![]() ,
,
综上所述,b的取值范围( ![]() ,
, ![]() )
)
【解析】(Ⅰ)求出函数的导数,得到x2=2x1﹣2,由a= ![]() ,设g(x)=
,设g(x)= ![]() ,根据函数的单调性求出a的最大值即可;(Ⅱ)求出函数的导数,问题转化为F′(x)=ex﹣2bx﹣c在(0,2)内至少有两个零点,通过讨论b的范围,求出函数的单调区间,从而确定b的范围即可.
,根据函数的单调性求出a的最大值即可;(Ⅱ)求出函数的导数,问题转化为F′(x)=ex﹣2bx﹣c在(0,2)内至少有两个零点,通过讨论b的范围,求出函数的单调区间,从而确定b的范围即可.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直线的参数方程为 ![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当 ![]() 时,|PA|+|PB|的值.
时,|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(1)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(2)在(1)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(3)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图. (Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172cm以上(含172cm)的人数;
(Ⅲ)在这50名男生身高在172cm以上(含172cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ﹣N(μ,σ2),则p(μ﹣σ<ξ≤μ+σ)=0.6826,p(μ﹣2σ<ξ≤μ+2σ)=0.9544,p(μ﹣3σ<ξ≤μ+3σ)=0.9974.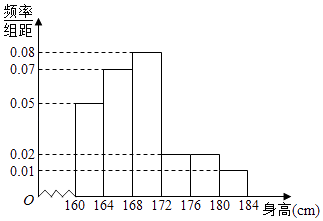
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 . (参考数据:sin15°=0.2588,sin7.5°=0.1305) 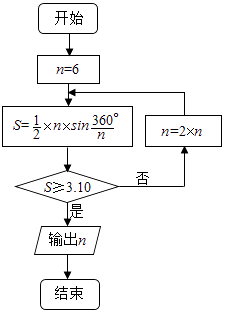
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+m|x+a|. (Ⅰ)当m=a=﹣1时,求不等式f(x)≥x的解集;
(Ⅱ)不等式f(x)≥2(0<m<1)恒成立时,实数a的取值范围是{a|a≤﹣3或a≥3},求实数m的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 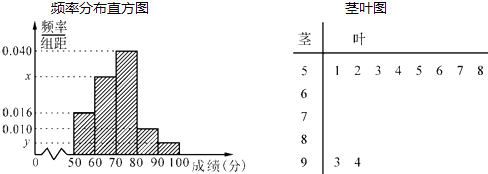
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设ξ表示所抽取的3名同学中得分在[80,90)的学生个数,求ξ的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos2ωx的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,若y=g(x)在
个单位,得到函数y=g(x)的图象,若y=g(x)在 ![]() 上为减函数,则正实数ω的最大值为( )
上为减函数,则正实数ω的最大值为( )
A.![]()
B.1
C.![]()
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com