
【题目】已知函数 ,函数
,函数![]() 有四个不同的零点,从小到大依次为
有四个不同的零点,从小到大依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
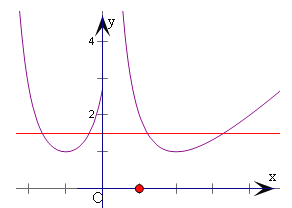
【解析】分析:通过f(x)的单调性,画出f(x)的图象和直线y=a,考虑四个交点的情况,得到x1=-2-x2,-1<x2≤0,x3x4=4,再由二次函数的单调性,可得所求范围.
详解:当x>0时,f(x)=![]() ,
,
可得f(x)在x>2递增,在0<x<2处递减,
由f(x)=e(x+1)2,x≤0,
x<-1时,f(x)递减;-1<x<0时,f(x)递增,
可得x=-1处取得极小值1,
作出f(x)的图象,以及直线y=a,
可得e(x1+1)2=e(x2+1)2=![]() ,
,
即有x1+1+x2+1=0,可得x1=-2-x2,-1<x2≤0,
![]()
可得x3x4=4,
x1x2+x3x4=4-2x2-x22=-(x2+1)2+5,在-1<x2≤0递减,
可得所求范围为[4,5).
故选B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , x∈R.
(1)若直线y=kx+1与f (x)的反函数g(x)=lnx的图象相切,求实数k的值;
(2)设x>0,讨论曲线y=f (x) 与曲线y=mx2(m>0)公共点的个数.
(3)设a<b,比较 ![]() 与
与 ![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列 ![]() 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列;
其中真命题是( )
A.p1 , p2
B.p3 , p4
C.p2 , p3
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=
的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF= ![]() ,则C的离心率e= .
,则C的离心率e= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面斜坐标系![]() 中,
中,![]() ,平面上任意一点
,平面上任意一点![]() 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若![]() (其中
(其中![]() ,
,![]() 分别为与
分别为与![]() 轴,
轴,![]() 轴同方向的单位向量),则
轴同方向的单位向量),则![]() 点的斜坐标为
点的斜坐标为![]()

(1)若点![]() 在斜坐标系
在斜坐标系![]() 中的坐标为
中的坐标为![]() ,求点
,求点![]() 到原点
到原点![]() 的距离.
的距离.
(2)求以原点![]() 为圆心且半径为
为圆心且半径为![]() 的圆在斜坐标系
的圆在斜坐标系![]() 中的方程.
中的方程.
(3)在斜坐标系![]() 中,若直线
中,若直线![]() 交(2)中的圆于
交(2)中的圆于![]() 两点,则当
两点,则当![]() 为何值时,
为何值时,![]() 的面积取得最大值?并求此最大值.
的面积取得最大值?并求此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日.第一届“一带一路国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年” 的人数之比为9:11

(1)根据已知条件完成上面的列联表,并判断能否有99%的把握认为关注“一带一路”是和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查,在这9人中再取3人进打面对面询问,记选取的3人中“一带一路”的人数为X,求x的分布列及数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com