
| A. | (-∞,-6) | B. | (-∞,-6)∪(6,+∞) | C. | (6,+∞) | D. | (-6,6) |
分析 原方程等价于x3+a=$\frac{4}{x}$,原方程的实根是曲线y=x3+a与曲线y=$\frac{4}{x}$的交点的横坐标:分a>0与a<0讨论,利用数形结合即可得到结论.
解答 解:方程的根显然x≠0,原方程等价于x3+a=$\frac{4}{x}$,
原方程的实根是曲线y=x3+a与曲线y=$\frac{4}{x}$的交点的横坐标;
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的.
若交点(xi,$\frac{4}{{x}_{i}}$)(i=1,2,k)均在直线y=x的同侧,
因直线y=x3与y=$\frac{4}{x}$交点为:(-2,-2),(2,2);

所以结合图象可得:$\left\{\begin{array}{l}{a>0}\\{{x}^{3}+a>-2}\\{x≥-2}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{{x}^{3}+a<2}\\{x≤2}\end{array}\right.$
解得a>6或a<-6,即实数a的取值范围是(-∞,-6)∪(6,∞),
故选:B
点评 本题考查函数与方程的综合运用,利用数形结合是解决本题的关键.注意合理地进行等价转化.


科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点M($\sqrt{3}$,$\sqrt{2}$)在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且点M到两焦点的距离之和为6.
如图,点M($\sqrt{3}$,$\sqrt{2}$)在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且点M到两焦点的距离之和为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
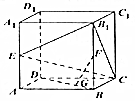 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com