
(1)用定义证明f(x)在[-1,1]上是增函数;
(2)解不等式f(x+![]() )<f(
)<f(![]() );
);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
(1)证明:任取-1≤x1<x2≤1,则
f(x1)-f(x2)=f(x1)+f(-x2)=![]() ·(x1-x2).
·(x1-x2).
∵-1≤x1<x2≤1,
∴x1+(-x2)≠0.
由已知![]() >0,
>0,
又x1-x2<0,∴f(x1)-f(x2)<0,即f(x)在[-1,1]上为增函数.
(2)解:∵f(x)在[-1,1]上为增函数,
故有 解得{x|-
解得{x|-![]() ≤x<-1}.
≤x<-1}.
(3)解:由(1)可知:f(x)在[-1,1]上是增函数,且f(1)=1,故对x∈[-1,1],恒有f(x)≤1.
所以要使f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,即要t2-2at+1≥1成立,故t2-2at≥0成立.
记g(a)=t2-2at,对a∈[-1,1],g(a)≥0恒成立,只需g(a)在[-1,1]上的最小值大于零.
故![]() 或
或![]()
解得t≥2或t≤-2或t=0.
讲评:本题主要考查不等式的解法及其应用,解不等式的应用非常广泛,如求函数的定义域、值域,求参数的取值范围等,高考试题中,对于解不等式要求较高,往往与函数概念,特别是二次函数、指数函数、对数函数等有关概念和性质密切相关.因此要求掌握不等式的基本性质,对各种类型的不等式的解法熟练掌握,提高运算化简能力.


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A.2 B.1 C.0 D.-1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R,满足f(a·b)=af(b)+bf(a),f(2)=2,a![]() =
=![]() (n∈N*),b
(n∈N*),b![]() =
=![]() (n∈N*);考查下列结论:
(n∈N*);考查下列结论:
①f(0)=f(1);②f(x)为偶函数;③数列{a![]() }为等比数列;④{b
}为等比数列;④{b![]() }为等差数列.
}为等差数列.
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一第一次阶段考试数学试卷(解析版) 题型:解答题
(本小题满分14分)已知f(x)是定义在( 0,+∞)上的增函数,
且f( ) =
f(x)-f(y)
) =
f(x)-f(y)
(1)求f(1)的值;
(2)若f(6)= 1,解不等式 f( x+3 )-f(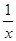 ) <2
) <2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com