
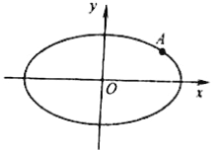
【题目】如图,在平面直角坐标系xOy中,椭圆E:![]() 的离心率为
的离心率为![]() ,点A(2,1)是椭圆E上的点.
,点A(2,1)是椭圆E上的点.
(1)求椭圆E的方程;
(2)过点A作两条互相垂直的直线l1,l2分別与椭圆E交于B,C两点,己知△ABC的面积为![]() ,求直线BC的方程.
,求直线BC的方程.
【答案】(1)![]() (2)x=
(2)x=![]() 或x-4y-2=0
或x-4y-2=0
【解析】
(1)将点![]() 的坐标代入椭圆方程,结合
的坐标代入椭圆方程,结合![]() ,解方程组求得
,解方程组求得![]() 的值,从而得到椭圆方程.(2)首先考虑直线
的值,从而得到椭圆方程.(2)首先考虑直线![]() 斜率不存在的情况,此时面积不合题意.当直线
斜率不存在的情况,此时面积不合题意.当直线![]() 斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出
斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出![]() ,同理求得
,同理求得![]() ,再用三角形面积为
,再用三角形面积为![]() 列方程,求得直线的斜率,由此求得
列方程,求得直线的斜率,由此求得![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 的方程.
的方程.
解:(1) 因为椭圆E的离心率为![]() ,所以
,所以![]() =
=![]() ,
,
又因为a2=b2+c2=2c2,所以a2=2b2=2c2,
因为点A(2,1)是椭圆E上的点,所以![]() +
+![]() =1
=1
解得b2=3,a2=6,
所以椭圆E的标准方程是![]() +
+![]() =1.
=1.
(2)当AB的斜率不存在或为0时,AB=4或2,此时△ABC的面积为4,不合题意舍去;
当AB的斜率存在且不为0时,设AB的斜率为k,则直线AB方程为y-1=k(x-2),
由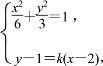 解得
解得![]() 或
或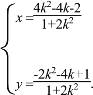
AB=![]() |
|![]() -2|=
-2|=![]() |
|![]() |,
|,
同理将上式中的k用-![]() 替换,得AC=
替换,得AC=![]() |
|![]() |,
|,
因为△ABC的面积为![]() ,所以
,所以![]() AB AC=
AB AC=![]()
![]() |
|![]() |
|![]() |
|![]() |=
|=![]() ,
,
化简得![]() =
=![]() ,
,
当k2≥1时,原方程可化为8k4-25k2-28=0,解得k2=4,
当k2≤1时,解得k2=![]() ,
,
即k=2或-2或![]() 或-
或-![]() ,
,
当AB的斜率2时,AC的斜率-![]() ,此时B点坐标(
,此时B点坐标(![]() ,-
,-![]() ),C点坐标(
),C点坐标(![]() ,
,![]() ),
),
此时直线BC的方程为x=![]() ,
,
当AB的斜率-2时,AC的斜率![]() ,此时B点坐标(
,此时B点坐标(![]() ,
,![]() ),C点坐标(-2,-1),
),C点坐标(-2,-1),
此时直线BC的方程为x-4y-2=0,
综上,直线BC的方程为x=![]() 或x-4y-2=0.
或x-4y-2=0.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,
中, ![]() ,其前
,其前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的各项均为正数,
的各项均为正数, ![]() ,且
,且![]() ,
, ![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令 ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() (
(![]() )的最大值与最小值.
)的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台有一档益智答题类综艺节日,每期节目从现场编号为01~80的80名观众中随机抽取10人答题.答题选手要从“科技”和“文艺”两类题目中选一类作答,一共回答10个问题,答对1题得1分.
(1)若采用随机数表法抽取答题选手,按照以下随机数表,从下方带点的数字2开始向右读,每次读取两位数,一行用完接下一行左端,求抽取的第6个观众的编号.
1622779439 4954435482 1737932378 8735![]() 09643 8426349164
09643 8426349164
8442175331 5724550688 7704744767 2176335025 8392120676
(2)若采用等距系统抽样法抽取答题选手,且抽取的最小编号为06,求抽取的最大编号.
(3)某期节目的10名答题选手中6人选科技类题目,4人选文艺类题目.其中选择科技类的6人得分的平均数为7,方差为![]() ;选择文艺类的4人得分的平均数为8,方差为
;选择文艺类的4人得分的平均数为8,方差为![]() .求这期节目的10名答题选手得分的平均数和方差.
.求这期节目的10名答题选手得分的平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
(1)证明函数![]() 是“正函数”;
是“正函数”;
(2)如果函数![]() 不是“正函数”,求正数a的取值范围.
不是“正函数”,求正数a的取值范围.
(3)如果函数 是“正函数”,求正数a的取值范围.
是“正函数”,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 都是各项为正数的数列,且
都是各项为正数的数列,且![]() ,
,![]() .对任意的正整数n,都有
.对任意的正整数n,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若存在p>0,使得集合M=![]() 恰有一个元素,求实数
恰有一个元素,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com