
【题目】对于数集![]() ,其中
,其中![]() ,
, ![]() ,定义向量集
,定义向量集![]() .若对于任意
.若对于任意![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .例如
.例如![]() 具有性质
具有性质![]() .
.
(![]() )若
)若![]() ,且
,且![]() 具有性质
具有性质![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 具有性质
具有性质![]() ,求证:
,求证: ![]() ,且当
,且当![]() 时,
时, ![]() .
.
(![]() )若
)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() (
(![]() 为常数),求有穷数列
为常数),求有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的通项公式.
的通项公式.
【答案】(1)1;(2)见解析;(3)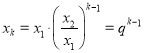 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(Ⅰ)由于具有该性质,所以必有任意向量都存在垂直向量,可以求出![]() 值。
值。
(Ⅱ)取![]() ,设
,设![]() 满足
满足![]() ,可得
,可得![]() ,
, ![]() 、
、![]() 中之一为-1,另一为1,故1X,然后只要用反证法证明
中之一为-1,另一为1,故1X,然后只要用反证法证明![]() 之间不存在即可;
之间不存在即可;
(Ⅲ)可以利用后一项比前一项的比值建立数集,最终求出后一项与前一项比是定值,从而是等比数列.
试题解析:
(1)选取![]() ,Y中与
,Y中与![]() 垂直的元素必有形式
垂直的元素必有形式![]() .
.
所以x=2b,从而x=4.
(2)证明:取![]() .设
.设![]() 满足
满足![]() .
.
由![]() 得
得![]() ,所以
,所以![]() 、
、![]() 异号.
异号.
因为-1是X中唯一的负数,所以![]() 、
、![]() 中之一为-1
中之一为-1
故1X.
假设![]() ,其中
,其中![]() ,则
,则![]() .
.
选取![]() ,并设
,并设![]() 满足
满足![]() ,即
,即![]() ,
,
则![]() 、
、![]() 异号,从而
异号,从而![]() 、
、![]() 之中恰有一个为-1.
之中恰有一个为-1.
若![]() =-1,则
=-1,则![]() ,矛盾;
,矛盾;
若![]() =-1,则
=-1,则![]() ,矛盾.
,矛盾.
所以x1=1.
(3)设![]() ,
,![]() ,则
,则![]() 等价于
等价于![]() 。
。
记![]() ,则数集
,则数集![]() 具有性质
具有性质![]() 当且仅当数集
当且仅当数集![]() 关于原点对称。
关于原点对称。
注意到![]() 是
是![]() 中的唯一负数,
中的唯一负数,![]() 共有
共有![]() 个数,所以
个数,所以![]() 也只有
也只有![]() 个数。
个数。
由于,已有![]() 个数,对以下三角数阵,
个数,对以下三角数阵,
![]() ,
,![]()
![]() 。
。
注意到![]() ,所以
,所以![]() ,从而数列的通项为
,从而数列的通项为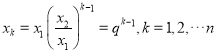 。
。


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:面![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知四棱锥![]() 的底面ABCD是边长为2的正方形,
的底面ABCD是边长为2的正方形,![]() 底面ABCD,E,F分别为棱BC,AD的中点.
底面ABCD,E,F分别为棱BC,AD的中点.

![]() 若
若![]() ,求异面直线PB和DE所成角的余弦值.
,求异面直线PB和DE所成角的余弦值.
![]() 若二面角
若二面角![]() 的余弦值为
的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过P点作圆M的切线
,点P在直线l上,过P点作圆M的切线![]() ,
,![]() ,切点为A,B.
,切点为A,B.
(1)若![]() ,试求点P的坐标;
,试求点P的坐标;
(2)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标;
(3)设线段![]() 的中点为N,求点N的轨迹方程.
的中点为N,求点N的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(-2,1),
=(-2,1),![]() =(x,y).
=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足![]() 的概率;
的概率;
(2)若x,y在区间[1,6]内取值,求满足![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若1路、2路公交车均途经泉港一中校门口,其中1路公交车每10分钟一趟,2路公交车每20分钟一趟,某生去坐这2趟公交车回家,则等车不超过5分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F(1,0),抛物线E:x2=2py的焦点为M.
(1)若过点M的直线l与抛物线C有且只有一个交点,求直线l的方程;
(2)若直线MF与抛物线C交于A,B两点,求△OAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的须率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.

(1)求成绩在50-70分的频率是多少
(2)求这三个年级参赛学生的总人数是多少:
(3)求成绩在80-100分的学生人数是多少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com