
����Ŀ������һ��ˮƽ���ԡ���ϵͳ�����ķ�����ȡ��50��ѧ������ѧ�ɼ��������з������о�����ͳ�Ƴɼ��ķ��鼰�����Ƶ�����£�![]() ��2��
��2��![]() ��3��
��3��![]() ��10��
��10��![]() ��15��
��15��![]() ��12��
��12��![]() ��8.
��8.
������Ƶ�ʷֲ���
���� | Ƶ�� | Ƶ�� |
| 2 | |
| 3 | |
| 10 | |
| 15 | |
| 12 | |
| 8 | |
�ϼ� | 50 |
Ƶ�ʷֲ�ֱ��ͼΪ
���������������Ƶ�ʷֲ���������Ƶ�ʷ�ֱ��ͼ��
���������Ƴɼ���85�����µ�ѧ��������
�������������������Ϣȥ������������������λ����ƽ����.����ȷ��0.01��
���𰸡���I������⣻��II��![]() ����III������
����III������![]() �����
����λ��![]() ��ƽ����
��ƽ����![]() .
.
��������
�����������������ݣ��ֱ�ó�ÿ���Ƶ�ʣ����ɵó�Ƶ�ʷֲ����������ɻ���Ƶ�ʷֲ�ֱ��ͼ��
��II������Ƶ�ʷֲ��������Ƴɼ���85�����µ�Ƶ����������ȷ����Ӧ��Ƶ�ʣ�
��III��������������λ�����Լ�ƽ�����ĸ�����Ƶ�ʷֲ�ֱ��ͼ�����ɷֱ��������.
��I��������ɵã�Ƶ�ʷֲ������£�
���� | Ƶ�� | Ƶ�� |
| 2 |
|
| 3 |
|
| 10 |
|
| 15 |
|
| 12 |
|
| 8 |
|
�ϼ� | 50 |
|
����Ƶ�ʷֲ�ֱ��ͼ���£�
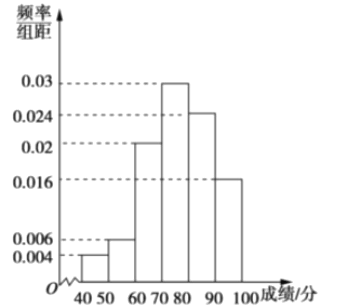
��II����Ƶ�ʷֲ�����֪���ɼ���![]() �����µ�Ƶ��Ϊ
�����µ�Ƶ��Ϊ![]() ��
��
���ԣ����Ƴɼ���![]() �����µ�ѧ������Ϊ
�����µ�ѧ������Ϊ![]() ��
��
��III����Ƶ�ʷֲ�ֱ��ͼ��֪��������ߵ�һ��Ϊ![]() ����������Ϊ
����������Ϊ![]() ��
��
����ʼǰ����С���ε����֮��Ϊ![]() ��������λ��λ�ڵ����飬
��������λ��λ�ڵ����飬
����λ��Ϊ![]() ����
����![]() ����ã�
����ã�![]() ��
��
������λ��ԼΪ![]() ��
��
ƽ����Ϊ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������ǣ� ��
A. ���⡰��![]() ����
����![]() ���������������
���������������![]() ����
����![]() ��
��
B. ������![]() ��
��![]() ��
�� ![]() ����������
����������![]() �ķ�Ϊ��
�ķ�Ϊ��![]() ��
�� ![]() ��
��
C. ��![]() ���ǡ�
���ǡ�![]() ���ij�ֲ���Ҫ����
���ij�ֲ���Ҫ����
D. ��![]() ���ǡ�ֱ��
���ǡ�ֱ��![]() ��ֱ��
��ֱ��![]() ��Ϊ��ֱ���ij�Ҫ����
��Ϊ��ֱ���ij�Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() .
.
��1����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
��2��������![]() �ķ���
�ķ���![]() �Ľ⼯��ǡ����һ��Ԫ�أ���ʵ��
�Ľ⼯��ǡ����һ��Ԫ�أ���ʵ��![]() ��ֵ��
��ֵ��
��3����![]() ����������
����������![]() ������
������![]() ������
������![]() �ϵ����ֵ����Сֵ�IJ����
�ϵ����ֵ����Сֵ�IJ����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���ͼ��ʾ�ij����ͼ�������������Ϊ141�����жϿ���Ӧ���������Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����E��F��G�ֱ���������ABCD��A1B1C1D1����AB��BC��B1C1���е㣬��ͼ��ʾ�������������е���������________(д������������ı��)��
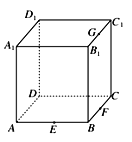
����������Ķ���Ϊ������������ĸ��������ֻ����������ֱ�������Σ�
������F��D1��G�Ľ����������Σ�
����P��ֱ��FG���˶�ʱ������AP��DE��
����Q��ֱ��BC1���˶�ʱ������A��D1QC������Ƕ�ֵ��
����M���������ƽ��A1B1C1D1�ڵĵ���D��C1������ȵĵ㣬���M�Ĺ켣��һ���߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ���ABCDΪֱ�����Σ�AD//BC����![]() ��BC��DC����BAD=60�㣬ƽ��PAD������ABCD��EΪAD���е㣬��PADΪ�ȱ������Σ�M����PC�ϵ�һ�㣬��
��BC��DC����BAD=60�㣬ƽ��PAD������ABCD��EΪAD���е㣬��PADΪ�ȱ������Σ�M����PC�ϵ�һ�㣬��![]() ��M��C���غϣ���
��M��C���غϣ���
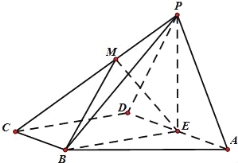
��1����֤��CD��DP��
��2����PA��ƽ��BME����k��ֵ��
��3���������M��BE��A��ƽ���Ϊ150�㣬��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊʵ������
Ϊʵ������
��1����![]() ʱ���жϺ���
ʱ���жϺ���![]() �ĵ����ԣ����ö���֤����
�ĵ����ԣ����ö���֤����
��2������![]() �IJ�ͬȡֵ������
�IJ�ͬȡֵ������![]() ����ż�ԣ���˵�����ɣ�
����ż�ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ����
����![]() ����
����![]() .
.
��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ������
������![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��3����![]() ʱ��
ʱ��![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ����ƽ�����Բ��
����ƽ�����Բ��![]() ����ƽ�洹ֱ��
����ƽ�洹ֱ��![]() ��
��![]() ������
������![]() ��
��![]() �ĵ���
�ĵ���
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��˵��������
��˵��������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com