
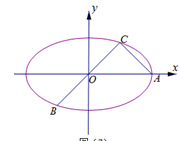
如图所示,已知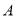 、
、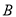 、
、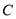 是长轴长为
是长轴长为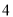 的椭圆
的椭圆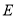 上的三点,点
上的三点,点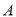 是长轴的一个端点,
是长轴的一个端点,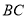 过椭圆中心
过椭圆中心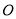 ,且
,且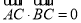 ,
, .
.
(1)求椭圆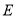 的方程;
的方程;
(2)在椭圆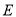 上是否存点
上是否存点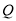 ,使得
,使得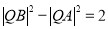 ?若存在,有几个(不必求出
?若存在,有几个(不必求出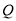 点的坐标),若不存在,请说明理由;
点的坐标),若不存在,请说明理由;
(3)过椭圆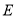 上异于其顶点的任一点
上异于其顶点的任一点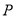 ,作圆
,作圆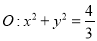 的两条线,切点分别为
的两条线,切点分别为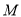 、
、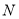 ,,若直线
,,若直线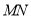 在
在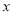 轴、
轴、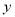 轴上的截距分别为
轴上的截距分别为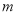 、
、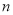 ,证明:
,证明: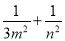 为定值.
为定值.
(1)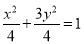 ;(2)存在,且有两个;(3)详见解析.
;(2)存在,且有两个;(3)详见解析.
【解析】
试题分析:(1)根据题中条件得到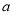 值,然后根据题中的几何条件得出点
值,然后根据题中的几何条件得出点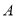 的坐标,代入椭圆方程求出
的坐标,代入椭圆方程求出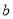 值,从而确定椭圆
值,从而确定椭圆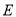 的方程;(2)解法一是设点
的方程;(2)解法一是设点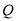 的坐标,利用两点间的距离公式将等式
的坐标,利用两点间的距离公式将等式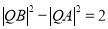 转化为点
转化为点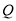 的坐标所满足的直线方程,注意到直线过椭圆内一定点,从而确定满足条件的点
的坐标所满足的直线方程,注意到直线过椭圆内一定点,从而确定满足条件的点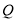 的个数;解法二是也是设点
的个数;解法二是也是设点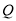 的坐标,利用两点间的距离公式将等式
的坐标,利用两点间的距离公式将等式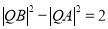 转化为点
转化为点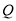 的坐标所满足的直线方程,再将直线方程与椭圆方程联立,利用
的坐标所满足的直线方程,再将直线方程与椭圆方程联立,利用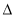 的正负确定所满足条件的点
的正负确定所满足条件的点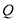 的个数;(3)设点
的个数;(3)设点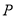 的坐标,先根据题中条件结合圆的几何性质得到
的坐标,先根据题中条件结合圆的几何性质得到 ,
, ,从而得出
,从而得出 、
、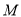 、
、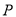 、
、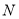 四点共圆,并写出圆
四点共圆,并写出圆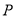 (以
(以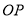 的长为半径的圆)的方程,通过将点
的长为半径的圆)的方程,通过将点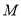 、
、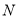 的坐标代入圆的方程,将两个等式相减的办法得到直线
的坐标代入圆的方程,将两个等式相减的办法得到直线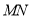 的方程,进而求出
的方程,进而求出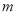 、
、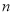 (由点
(由点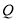 的坐标表示),并将点
的坐标表示),并将点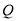 的坐标由
的坐标由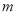 、
、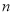 表示,再将点
表示,再将点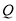 的坐标代入椭圆的方程化简即可证明相关问题;解法二是设
的坐标代入椭圆的方程化简即可证明相关问题;解法二是设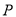 、
、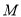 、
、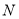 三点的坐标,利用圆的几何性质得到
三点的坐标,利用圆的几何性质得到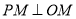 ,先利用点斜式写出直线
,先利用点斜式写出直线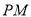 的方程,同时写出直线
的方程,同时写出直线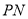 的方程,再将点
的方程,再将点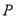 代入上述两直线的方程,通过比较得出直线
代入上述两直线的方程,通过比较得出直线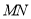 的方程,进而求出
的方程,进而求出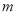 、
、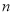 (由点
(由点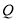 的坐标表示),并将点
的坐标表示),并将点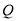 的坐标由
的坐标由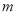 、
、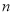 表示,再将点
表示,再将点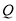 的坐标代入椭圆的方程化简即可证明相关问题.
的坐标代入椭圆的方程化简即可证明相关问题.
试题解析:(1)依题意知:椭圆的长半轴长 ,则
,则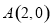 ,
,
设椭圆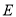 的方程为
的方程为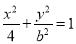 ,
,
由椭圆的对称性知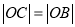 又
又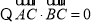 ,
,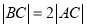 ,
,
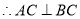 ,
,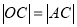 ,
,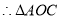 为等腰直角三角形,
为等腰直角三角形,
 点
点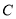 的坐标为
的坐标为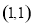 ,点
,点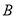 的坐标为
的坐标为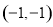 ,
,
将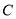 的坐标
的坐标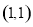 代入椭圆方程得
代入椭圆方程得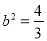 ,
,
 所求的椭圆
所求的椭圆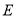 的方程为
的方程为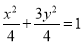 ;
;
(2)解法一:设在椭圆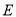 上存在点
上存在点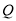 ,使得
,使得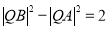 ,设
,设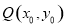 ,则
,则
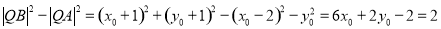 ,
,
即点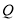 在直线
在直线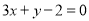 上,
上,
 点
点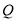 即直线
即直线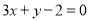 与椭圆
与椭圆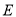 的交点,
的交点,
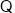 直线
直线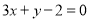 过点
过点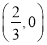 ,而点椭圆
,而点椭圆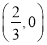 在椭圆
在椭圆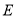 的内部,
的内部,
 满足条件的点
满足条件的点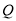 存在,且有两个;
存在,且有两个;
解法二:设在椭圆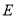 上存在点
上存在点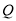 ,使得
,使得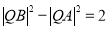 ,设
,设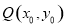 ,则
,则
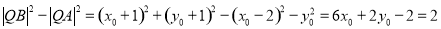 ,
,
即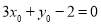 ,①
,①
又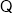 点
点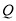 在椭圆
在椭圆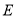 上,
上,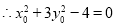 ,②
,②
由①式得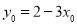 代入②式并整理得:
代入②式并整理得: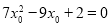 ,③
,③
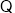 方程③的根判别式
方程③的根判别式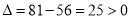 ,
,
 方程③有两个不相等的实数根,即满足条件的点
方程③有两个不相等的实数根,即满足条件的点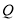 存在,且有两个;
存在,且有两个;
(3)解法一:设点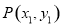 ,由
,由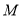 、
、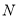 是圆
是圆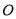 的切点知,
的切点知, ,
, ,
,

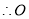 、
、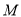 、
、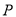 、
、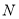 四点在同一圆上,
四点在同一圆上,
且圆的直径为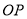 ,则圆心为
,则圆心为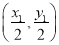 ,
,
其方程为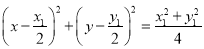 ,
,
即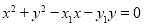 ,④
,④
即点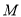 、
、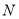 满足方程④,又点
满足方程④,又点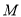 、
、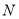 都在圆
都在圆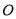 上,
上,
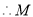 、
、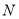 坐标也满足圆
坐标也满足圆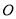 的方程
的方程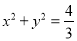 ,⑤
,⑤
⑤ ④得直线
④得直线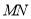 的方程为
的方程为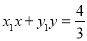 ,
,
令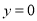 ,得
,得 ,令
,令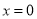 得
得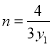 ,
,
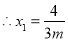 ,
,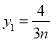 ,又点
,又点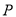 在椭圆
在椭圆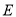 上,
上,
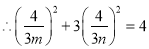 ,即
,即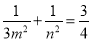 (定值);
(定值);
解法二:设点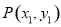 、
、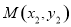 、
、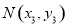 ,则
,则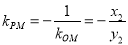 ,
,
直线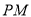 的方程为
的方程为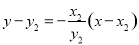 ,化简得
,化简得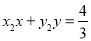 ,④
,④
同理可得直线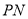 的方程为
的方程为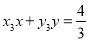 ,⑤把
,⑤把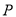 点的坐标代入④、⑤得
点的坐标代入④、⑤得 ,
,
 直线
直线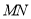 的方程为
的方程为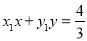 ,
,
令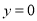 ,得
,得 ,令
,令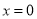 得
得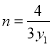 ,
,
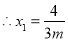 ,
,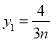 ,又点
,又点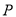 在椭圆
在椭圆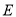 上,
上,
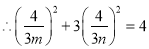 ,即
,即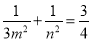 (定值).
(定值).
考点:1.椭圆的方程;2.直线与圆、圆锥曲线的位置关系;3.直线的方程


科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,则该几何体的体积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数又在区间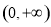 上存在零点的是( )
上存在零点的是( )
A. B.
B.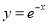 C.
C.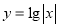 D.
D.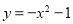
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:填空题
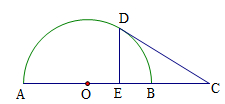
如图,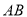 是半圆的直径,
是半圆的直径,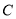 是
是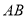 延长线上一点,
延长线上一点,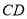 切半圆于点
切半圆于点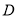 ,
,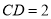 ,
, ,垂足为
,垂足为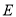 ,且
,且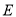 是
是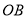 的中点,则
的中点,则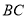 的长为 .
的长为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试理科数学试卷(解析版) 题型:选择题
定义一个集合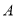 的所有子集组成的集合叫做集合
的所有子集组成的集合叫做集合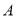 的幂集,记为
的幂集,记为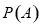 ,用
,用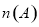 表示有限集
表示有限集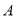 的元素个数,给出下列命题:①对于任意集合
的元素个数,给出下列命题:①对于任意集合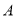 ,都有
,都有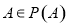 ;②存在集合
;②存在集合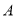 ,使得
,使得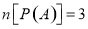 ;
;
③用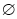 表示空集,若
表示空集,若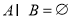 ,则
,则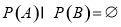 ;④若
;④若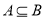 ,则
,则 ;⑤若
;⑤若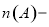
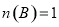 ,则
,则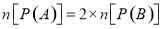 其中正确的命题个数为( )
其中正确的命题个数为( )
A.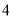 B.
B.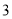 C.
C.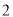 D.
D.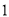
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:填空题
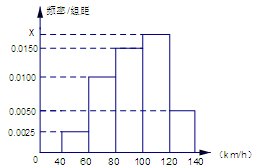
根据某固定测速点测得的某时段内过往的 辆机动车的行驶速度(单位:
辆机动车的行驶速度(单位: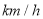 )绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为
)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为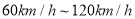 ,则该时段内过往的这
,则该时段内过往的这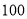 辆机动车中属非正常行驶的有辆,图中的
辆机动车中属非正常行驶的有辆,图中的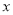 值为.
值为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
已知 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, .设函数
.设函数 ,当
,当 时,函数
时,函数 的值域为集合
的值域为集合 ,则
,则 中的元素个数为.
中的元素个数为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com