
【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上.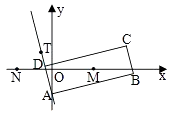
(1)AD边所在直线的方程;
(2)矩形ABCD外接圆的方程.
【答案】
(1)解: AB边所在直线的方程为x﹣3y﹣6=0,且AD与AB垂直,
∴直线AD的斜率为﹣3.又因为点T(﹣1,1)在直线AD上,
∴AD边所在直线的方程为y﹣1=﹣3(x+1),3x+y+2=0.
(2)由 ![]() ,解得点A的坐标为(0,﹣2),
,解得点A的坐标为(0,﹣2),
∵矩形ABCD两条对角线的交点为M(2,0).
∴M为矩形ABCD外接圆的圆心,又|AM|2=(2﹣0)2+(0+2)2=8,∴ ![]() .
.
从而矩形ABCD外接圆的方程为 (x﹣2)2+y2=8.
【解析】(1) AB的斜率确定,又AD与AB垂直可知AD的斜率为﹣3。点T(﹣1,1)在直线AD上, 代入直线方程的点斜式即可。
(2)由AD与AB的直线方程可求出A点坐标。以M(2,0)为圆心,以AM为半径的外接圆的方程即可确定。
【考点精析】本题主要考查了点斜式方程和圆的标准方程的相关知识点,需要掌握直线的点斜式方程:直线![]() 经过点
经过点![]() ,且斜率为
,且斜率为![]() 则:
则:![]() ;圆的标准方程:
;圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程才能正确解答此题.
;圆心为A(a,b),半径为r的圆的方程才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的y(y<5)的概率;
(3)求输出的y(6<y≤8)的概率.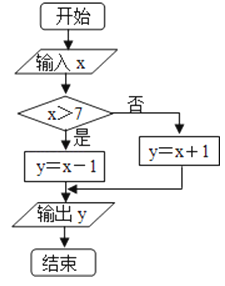
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南方
的正南方![]() 处,
处,![]() 千米,甲船以每小时
千米,甲船以每小时![]() 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自![]() 出发以每小时
出发以每小时![]() 千米的速度向北偏东
千米的速度向北偏东![]() 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
A. ![]() 分钟 B.
分钟 B. ![]() 分钟 C.
分钟 C. ![]() 分钟 D.
分钟 D. ![]() 分钟
分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则 ![]() 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com