
【题目】下列说法正确的是( )
A.命题“若x2=9,则x=±3”的否命题为“若x2=9,则x≠±3”
B.若命题P:?x0∈R, ![]() ,则命题?P:?x∈R,
,则命题?P:?x∈R, ![]()
C.设 ![]() 是两个非零向量,则“
是两个非零向量,则“ ![]() 是“
是“ ![]() 夹角为钝角”的必要不充分条件
夹角为钝角”的必要不充分条件
D.若命题P: ![]() ,则¬P:
,则¬P: ![]()
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式: 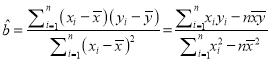 ,
, ![]()
参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() f.
f.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:(1)f(x)+f(2﹣x)=0,(2)f(x﹣2)=f(﹣x),(3)在[﹣1,1]上表达式为f(x)=  ,则函数f(x)与函数g(x)=
,则函数f(x)与函数g(x)= ![]() 的图象区间[﹣3,3]上的交点个数为( )
的图象区间[﹣3,3]上的交点个数为( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且满足4Sn﹣1=an2+2an , n∈N* .
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:
,数列{bn}的前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin3x,﹣y),
sin3x,﹣y), ![]() =(m,cos3x﹣m)(m∈R),且
=(m,cos3x﹣m)(m∈R),且 ![]() +
+ ![]() =
= ![]() .设y=f(x).
.设y=f(x).
(1)求f(x)的表达式,并求函数f(x)在[ ![]() ,
, ![]() ]上图象最低点M的坐标.
]上图象最低点M的坐标.
(2)在△ABC中,f(A)=﹣ ![]() ,且A>
,且A> ![]() π,D为边BC上一点,AC=
π,D为边BC上一点,AC= ![]() DC,BD=2DC,且AD=2
DC,BD=2DC,且AD=2 ![]() ,求线段DC的长.
,求线段DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为 ![]() ,答对文科题的概率均为
,答对文科题的概率均为 ![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分X的分布列与数学期望E(X).
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈(﹣∞,0),2x>3x;命题q:x∈(0, ![]() ),sinx>x,则下列命题为真命题的是( )
),sinx>x,则下列命题为真命题的是( )
A.p∧q
B.(¬p)∨q
C.(¬p)∧q
D.p∧(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com