
 ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.
 .
. 是正方形,知其两条对角线互相垂直平分,且
是正方形,知其两条对角线互相垂直平分,且 ,又因为平面
,又因为平面 平面
平面 ,
, 平面
平面 ,故可以以点
,故可以以点 为原点,以过
为原点,以过 点平行于
点平行于 的直线为
的直线为 轴,分别以直线
轴,分别以直线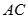 和
和 为
为 轴和
轴和 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 ;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量
;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量 的坐标,从而可证
的坐标,从而可证 ,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知
,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知 是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为
是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为 ,则由
,则由 且
且 ,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明.
,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明. 是正方形 ,
是正方形 ,  ,
, 平面
平面 ,
, 平面
平面 ,
,  为原点,以过
为原点,以过 点平行于
点平行于 的直线为
的直线为 轴,
轴, 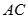 和
和 为
为 轴和
轴和 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 .
. ,则
,则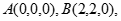
 ,
, 是正方形
是正方形 的对角线的交点,
的对角线的交点, .
.

 ,
, ,
, ,
, ,
, 
 平面
平面 .
.  的法向量为
的法向量为 ,则
,则 且
且 ,
,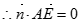 且
且 .
. 即
即
 ,则
,则 , 则
, 则 .
.  为平面
为平面 的一个法向量,且
的一个法向量,且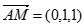 ,
, ,
, 的平面角为
的平面角为 ,则
,则 ,
, 等于
等于 .
.

科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| a |
| b |
| A.锐角三角形 |
| B.钝角三角形 |
| C.直角三角形 |
| D.形状与a,b的值有关的三角形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com