解:(1)∵f(x)=x|x-a|,
∴不等式f(x)<x即为x|x-a|<x
1
0显然x≠0,
2
0当x>0时原不等式可化为:|x-a|<1?-1<x-a<1?a-1<x<a+1
当a-1≥0即a≥1时得不等式的解为:a-1<x<a+1
当a-1<0即0<a<1时得不等式的解为:0<x<a+1
3
0当x<0时原不等式可化为:|x-a|>1?x-a>1或x-a<-1?x>a+1或x<a-1
当a≥1时,得不等式的解为x<0
当0<a<1时,得不等式的解为:x<a-1
综上得:当a≥1时,原不等式的解集为{x|x<0}∪{x|a-1<x<a+1}
当0<a<1时,原不等式的解集为{x|x<a-1}∪{x|0<x<a+1}
(2)∵对?x∈(0,1]都有f(x)<m,显然m>0
即-m<x(x-a)<m?对?x∈(0,1],-
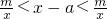
恒成立?对?x∈(0,1],x-
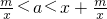
恒成立
设g(x)=x-

,x∈(0,1],p(x)=x+

,x∈(0,1]
则对?x∈(0,1],x-
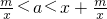
恒成立?g(x)
max<a<p(x)
min,x∈(0,1]
∵g(x)'=1+
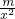
,当x∈(0,1]时g(x)'>0
∴函数g(x)在(0,1]上单调递增,∴g(x)
max=1-m
又∵p(x)'=1-
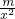
=
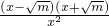
,
当

≥1即m≥1时,对于x∈(0,1],p(x)'<0
∴函数p(x)在(0,1]上为减函数,
∴p(x)
min=p(1)=1+m
当

<1,即0<m<1时,
当

,p(x)'≤0
当

,p(x)'>0
∴在(0,1]上,
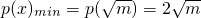
(或当0<m<1时,在(0,1]上,p(x)=x+

≥2

,当x=

时取等号)
又∵当0<m<1时,要g(x)
max<a<p(x)
min即1-m<a<2

还需满足2

>1-m解得3-2

<m<1
∴当3-2

<m<1时,1-m<a<2

;
当m≥1时,1-m<a<1+m.
分析:(1)本题关键在对x进行分类讨论的基础上,还要对a进行讨论
(2)若对?x∈(0,1]都有f(x)<m(m∈R,m是常数),则知对?x∈(0,1],

恒成立,然后根据导函数分别求出x-

,x

的最大值,最小值,最后再对m讨论得到最值,即可得到m的范围
点评:本题考查了二次函数在闭区间上的最值,一元二次不等式的解法,另外分类讨论也是解题的关键,属于基础题.

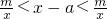 恒成立?对?x∈(0,1],x-
恒成立?对?x∈(0,1],x-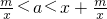 恒成立
恒成立 ,x∈(0,1],p(x)=x+
,x∈(0,1],p(x)=x+ ,x∈(0,1]
,x∈(0,1]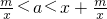 恒成立?g(x)max<a<p(x)min,x∈(0,1]
恒成立?g(x)max<a<p(x)min,x∈(0,1]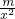 ,当x∈(0,1]时g(x)'>0
,当x∈(0,1]时g(x)'>0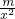 =
=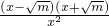 ,
, ≥1即m≥1时,对于x∈(0,1],p(x)'<0
≥1即m≥1时,对于x∈(0,1],p(x)'<0 <1,即0<m<1时,
<1,即0<m<1时, ,p(x)'≤0
,p(x)'≤0 ,p(x)'>0
,p(x)'>0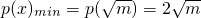
 ≥2
≥2 ,当x=
,当x= 时取等号)
时取等号) 还需满足2
还需满足2 >1-m解得3-2
>1-m解得3-2 <m<1
<m<1 <m<1时,1-m<a<2
<m<1时,1-m<a<2 ;
; 恒成立,然后根据导函数分别求出x-
恒成立,然后根据导函数分别求出x- ,x
,x 的最大值,最小值,最后再对m讨论得到最值,即可得到m的范围
的最大值,最小值,最后再对m讨论得到最值,即可得到m的范围

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<