
【题目】已知直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsinθ+3=0,A、B两点极坐标分别为(1,π)、(1,0).
(1)求曲线C的参数方程;
(2)在曲线C上取一点P,求|AP|2+|BP|2的最值.
【答案】
(1)解:曲线C的极坐标方程为ρ2﹣4ρsinθ+3=0,
把ρ2=x2+y2,y=ρsinθ代入可得C的直角坐标方程:x2+y2﹣4y+3=0,
配方为x2+(y﹣2)2=1,
可得参数方程: ![]() (α为参数)
(α为参数)
(2)解:A、B两点极坐标分别为(1,π)、(1,0),
分别化为直角坐标:(﹣1,0),(1,0).
令P(cosα,2+sinα),
则|AP|2+|BP|2=(cosα+1)2+(2+sinα)2+(cosα﹣1)2+(2+sinα)2=8sinα+12,
当sinα=﹣1时,有最小值4;当sinα=1时,有最大值20
【解析】(1)曲线C的极坐标方程为ρ2﹣4ρsinθ+3=0,把ρ2=x2+y2 , y=ρsinθ代入可得C的直角坐标方程,配方可得参数方程.(2)A、B两点极坐标分别为(1,π)、(1,0),分别化为直角坐标:(﹣1,0),(1,0).令P(cosα,2+sinα),则|AP|2+|BP|2=8sinα+12,利用sinα的值域即可得出最值.


科目:高中数学 来源: 题型:
【题目】已知定义在[﹣ ![]() ,
, ![]() ]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,满足
,满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD – A1B1C1D1中,点E,F,G分别是棱BC,A1B1,B1C1的中点.
(1)求异面直线EF与DG所成角的余弦值;
(2)设二面角A—BD—G的大小为θ,求 |cosθ| 的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的一条准线方程为x=
(a>b>0)的一条准线方程为x=![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
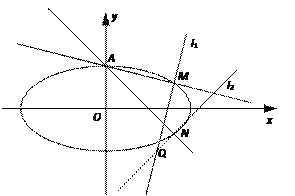
(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.
① 设直线AM,AN的斜率分别是k1, k2,求k1k2的值;
② 过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左右焦点分别为
,左右焦点分别为![]() 和
和![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与以点
为半径的圆与以点![]() 为圆心,以
为圆心,以![]() 为半径的圆相交,且交点在椭圆
为半径的圆相交,且交点在椭圆![]() 上.
上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设椭圆
)设椭圆![]() ,
, ![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
①求![]() 的值.
的值.
②(理科生做)求![]() 面积的最大值.
面积的最大值.
③(文科生做)当![]() 时,
时, ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (小时,
(小时,![]() )的函数
)的函数![]() 近似满足
近似满足![]() ,如图是函数
,如图是函数![]() 的部分图象(
的部分图象(![]() 对应凌晨
对应凌晨![]() 点).
点).

(Ⅰ)根据图象,求![]() 的值;
的值;
(Ⅱ)由于当地冬季雾霾严重,从环保的角度,既要控制火力发电厂的排放量,电力供应有限;又要控制企业的排放量,于是需要对各企业实行分时拉闸限电措施.已知该企业某日前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com