
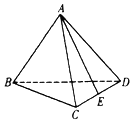
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 根据向量的几何意义和向量的数量积公式计算即可.
解答 解:∵正四面体ABCD的棱长为1,点E是棱CD的中点,
∴$\overrightarrow{AE}$•$\overrightarrow{AB}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AD}$)•$\overrightarrow{AB}$
=$\frac{1}{2}$$\overrightarrow{AC}$•$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$•$\overrightarrow{AB}$=$\frac{1}{2}$×1×1×$\frac{1}{2}$+$\frac{1}{2}$×1×1×$\frac{1}{2}$=$\frac{1}{2}$,
故选:D.
点评 本题主要考查向量的数量积运算,要求熟练掌握数量积的公式.


科目:高中数学 来源: 题型:解答题
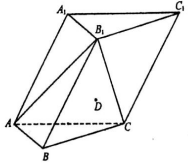 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意参加 | 不愿意参加 | 合计 | |
| 城填生 | 50 | 25 | 75 |
| 农村生 | 10 | 15 | 25 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )
如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )| A. | 50米 | B. | 25$\sqrt{3}$米 | C. | 25米 | D. | 50$\sqrt{3}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com