
 |OA||y|=
|OA||y|= .(2)见解析。
.(2)见解析。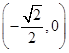 ,渐近线方程:y=±
,渐近线方程:y=±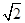 x,然后可设出过点A与渐近线y=
x,然后可设出过点A与渐近线y=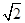 x平行的直线方程为y=
x平行的直线方程为y=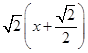 ,即y=
,即y=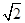 x+1.它再与另一条渐近线方程联立解方程组可求出交点坐标,从而得到所求三角形的高,度显然等于|OA|,面积得解.
x+1.它再与另一条渐近线方程联立解方程组可求出交点坐标,从而得到所求三角形的高,度显然等于|OA|,面积得解.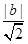 =1,即b2=2.
=1,即b2=2. 得x2-2bx-b2-1=0(*)
得x2-2bx-b2-1=0(*)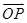 ·
· =x1x2+y1y2=x1x2+(x1+b)(x2+b)=2x1x2+b(x1+x2)+b2,借助(*)式方程中的韦达定理代入此式证明
=x1x2+y1y2=x1x2+(x1+b)(x2+b)=2x1x2+b(x1+x2)+b2,借助(*)式方程中的韦达定理代入此式证明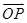 ·
· =0即可.
=0即可.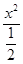 -y2=1,左顶点A
-y2=1,左顶点A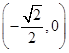 ,渐近线方程:y=±
,渐近线方程:y=±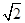 x.
x.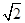 x平行的直线方程为y=
x平行的直线方程为y=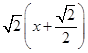 ,即y=
,即y=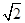 x+1.
x+1. 得
得
 |OA||y|=
|OA||y|= .
.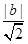 =1,即b2=2.
=1,即b2=2. 得x2-2bx-b2-1=0.
得x2-2bx-b2-1=0.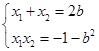
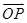 ·
· =x1x2+y1y2=2x1x2+b(x1+x2)+b2
=x1x2+y1y2=2x1x2+b(x1+x2)+b2

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com