
【题目】在某市高中某学科竞赛中,某一个区4000名考生的参赛成绩统计如图所示.
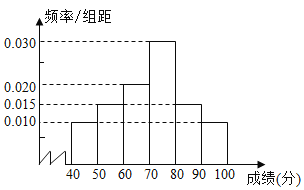
(1)求这4000名考生的竞赛平均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合计 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
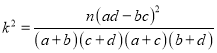 .
.
【答案】(1)![]() (2)见解析,有99%的把握认为有关.
(2)见解析,有99%的把握认为有关.
【解析】
(1)利用频率分布直方图,由每一组数据的中点值乘以该组的频率,进行求和即可求出这4000名考生的竞赛平均成绩![]() ;
;
(2)计算70分以上的频率和频数,由此填写列联表,并由表中数据求出![]() ,然后对照临界值判断即可.
,然后对照临界值判断即可.
(1)由题意,得:
中间值 | 45 | 55 | 65 | 75 | 85 | 95 |
概率 | 0.1 | 0.15 | 0.2 | 0.3 | 0.15 | 0.1 |
∴![]() ,
,
∴4000名考生的竞赛平均成绩![]() 为
为![]() .
.
(2)
由题意70分以上的频率为![]() ,
,
频数为![]() ,
,
70分及以下为![]() ,
,
由此填写列联表如下:
合格 | 优秀 | 合计 | |
男生 | 720 | 1180 | 1900 |
女生 | 1080 | 1020 | 2100 |
合计 | 1800 | 2200 | 4000 |
由表中数据可得,
![]() ,
,
![]() 有99%的把握认为有关.
有99%的把握认为有关.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ2﹣6ρcosθ+5=0,曲线C2的参数方程为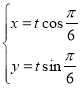 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程,并说明是什么曲线?
(2)若曲线C1与C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
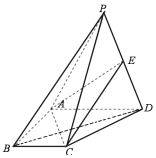
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
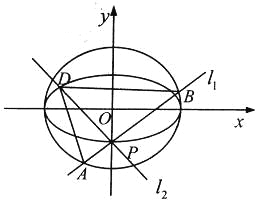
【题目】如图,点![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点,![]() 的长轴是圆
的长轴是圆![]() 的直径,
的直径,![]() 、
、![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的![]() 位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.
位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.

(Ⅰ)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(Ⅱ)若按分层抽样的方法从年龄在![]() 以内及
以内及![]() 以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在
以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),任意的![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
(1)求曲线C1的一般方程和曲线C2的直角坐标方程;
(2)若点P在曲线C1上,点Q曲线C2上,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的![]() 位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下所示.
位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下所示.
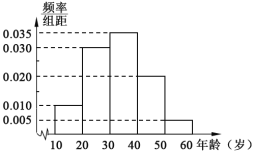
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在![]() 以及
以及![]() 内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽取的3人中,年龄在
内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽取的3人中,年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com