练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．下列关系中正确的个数为（　　）
    ①0∈{0}
    ②Φ?{0}
    ③{0，1}⊆{（0，1）}．
    A．0B．1C．2D．3

    分析 由空集的性质、元素和集合和集合和集合的关系，即可判断．

    解答 解：①0∈{0}正确；
    ②Φ?{0}，由空集是非空集合的真子集，故正确；
    ③{0，1}⊆{（0，1）}，错误，一个为数集，一个为点集．
    正确的个数为2．
    故选：C．

    点评 本题考查空集的性质、元素和集合和集合和集合的关系，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列说法，不正确的是（　　）
    A．平面A′FG⊥平面ABC
    B．BC∥平面A′DE
    C．三棱锥A′-DEF的体积最大值为$\frac{1}{64}{a^3}$
    D．直线DF与直线A′E有可能异面

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．命题p：?x0∈R，x0≤2的否定是（　　）
    A．￢p：?x∈R，x≤2B．￢p：?x∈R，x＞2C．￢p：?x∈R，x＞2D．￢p：?x∈R，x≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．如果直线y=kx-1与双曲线x2-y2=4的右支有两个公共点，求k的取值范围（　　）
    A．1＜k＜$\frac{\sqrt{5}}{2}$B．-$\frac{\sqrt{5}}{2}$＜k＜$\frac{\sqrt{5}}{2}$C．-$\frac{\sqrt{5}}{2}$＜k＜-1D．-$\frac{\sqrt{5}}{2}$＜k＜1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．定义运算a⊕b=$\left\{\begin{array}{l}a\begin{array}{l}{\;}，{a＜b}\end{array}\\ b\begin{array}{l}{\;}，{a≥b}\end{array}\end{array}$若函数f（x）=2x⊕2-x，则f（x）的值域是（　　）
    A．[1，+∞）B．（0，+∞）C．（0，1]D．$[{\frac{1}{2}，1}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数 y=x2+x（-1≤x≤3}的值域是（　　）
    A．[0，12]B．[-$\frac{1}{4}$，12]C．[-$\frac{1}{2}$，12]D．[$\frac{3}{4}$，12]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．类比平面内正三角形的“三边相等，三内角相等”的性质，可推出正四面体的下列哪些性质，你认为比较恰当的是（　　）
    ①各棱长相等，同一顶点上的任两条棱的夹角都相等；
    ②各个面都是全等的正三角形，相邻两个面所成的二面角都相等； 
    ③各个面都是全等的正三角形，同一顶点上的任两条棱的夹角都相等．
    A．①③B．②③C．①②D．①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

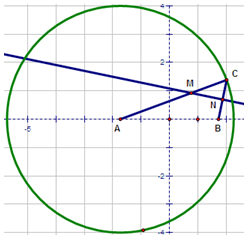    13．以$A（-\sqrt{3}，0）$为圆心，4为半径作圆，$B（\sqrt{3}，0）$，C为圆上任意一点，分别连接AC，BC，过BC的中点N作BC的垂线，交AC于点M，当点C在圆上运动时，
    （1）求M点的轨迹方程，并说明它是何种曲线；
    （2）求直线y=kx+1截（1）所得曲线弦长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在数列{an}中，a1=1，a2=2，且an+1=（1+q）an-qan-1（n≥2，q≠0）
    （Ⅰ）设bn=an+1-an（n∈N*），证明{bn}是等比数列；
    （Ⅱ）当q=2时，求数列{an}的通项公式．

    查看答案和解析>>

    同步练习册答案