
����Ŀ��������ϷԽ��Խ������ϲ��������ij�����Ƽ�����֯���������������ס��ҡ�����������ѧУ��ѧ����������������ѧ�������������ʾ��
��ѧ | �� | �� | �� | �� |
���� | 30 | 40 | 20 | 10 |
Ϊ�˽����ѧ��������ˮƽ���ÿƼ��ݲ��÷ֲ�����ķ�������������ѧ�IJ���ѧ���г�ȡ30���μ��ʾ����飮
�����ʼס��ҡ�������������ѧ����ȡ������ѧ����
���Ӳμ��ʾ������30��ѧ���������ȡ2��������2��ѧ������ͬһ����ѧ�ĸ��ʣ�
�����ڲμ��ʾ������30��ѧ���У������Լס���������ѧ��ѧ���������ȡ2������X��ʾ��ü���ѧ��ѧ����������X�ķֲ��У�
���𰸡��⣺����������֪��������ѧ�����μ�����������ѧ��������Ϊ100���� ��ȡ��������������������ı�ֵΪ ![]() ��
��
���Լס��ҡ�������������ѧ����ȡ��ѧ�������ֱ�Ϊ9��12��6��3��
�����衰��30��ѧ���������ȡ����ѧ����������ѧ������ͬһ����ѧ��Ϊ�¼�A��
��30��ѧ���������ȡ����ѧ����ȡ������ ![]() �֣�
�֣�
����ͬһ����ѧ��ȡ������ ![]() ��
��
���� ![]() ��
��
�𣺴�30��ѧ���������ȡ����ѧ������ͬһ����ѧ�ĸ���Ϊ ![]() ��
��
�����ɣ���֪��30��ѧ���У����Լס���������ѧ��ѧ�������ֱ�Ϊ9��6��
������ã�X�Ŀ���ȡֵΪ0��1��2��![]() ��
��![]() ��
��![]() ��
��
����X�ķֲ���Ϊ��
X | 0 | 1 | 2 |
P | | | |
������������������ѧ�����μ�����������ѧ��������Ϊ100������ȡ��������������������ı�ֵ ![]() ���ɴ�������ס��ҡ�������������ѧ����ȡ��ѧ������������30��ѧ���������ȡ����ѧ����ȡ������
���ɴ�������ס��ҡ�������������ѧ����ȡ��ѧ������������30��ѧ���������ȡ����ѧ����ȡ������ ![]() �֣�����ͬһ����ѧ��ȡ������
�֣�����ͬһ����ѧ��ȡ������ ![]() ���ɴ��������30��ѧ���������ȡ����ѧ������ͬһ����ѧ�ĸ��ʣ� ����������ã�X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
���ɴ��������30��ѧ���������ȡ����ѧ������ͬһ����ѧ�ĸ��ʣ� ����������ã�X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
�����㾫����������Ĺؼ���������ֲ���������֪ʶ�������Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ����������������������������Լ�����ɢ�������������ֲ��е����⣬�˽����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�� ![]() ��������
�������� ![]() ���ڵ�
���ڵ� ![]() ������Բ
������Բ ![]() �����������Ҳ�ĵ�
�����������Ҳ�ĵ� ![]() Ϊ�����ߵĽ��㣬��
Ϊ�����ߵĽ��㣬�� ![]() �����ֵΪ�� ��
�����ֵΪ�� ��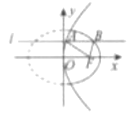
A.![]()
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ΪM���������ݣ���Ƶ�ʷֲ���������
��1������a,b��ֵ;
��2������Ƶ�ʷֲ�ֱ��ͼ��
��3����Ƶ�ʷֲ�ֱ��ͼ����������������ƽ�����Ĺ���ֵ��
Ƶ�ʷֲ���
���� | Ƶ�� | Ƶ�� | Ƶ��/��� |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��һ��ͼ����ͼ��ʾ����
��һ��ͼ����ͼ��ʾ����![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ��
��![]() ������λ���ɵõ�����
������λ���ɵõ�����![]() ��ͼ����ͼ�����ԭ��Գ�.��1����
��ͼ����ͼ�����ԭ��Գ�.��1����![]() ��ֵ.
��ֵ.
��2����![]() ����Сֵ����д��
����Сֵ����д��![]() �ı���ʽ.
�ı���ʽ.
(3)��t>0,����x���![]() ������
������![]() ����СֵΪ-2����t�ķ�Χ.
����СֵΪ-2����t�ķ�Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=ln��x2��x���Ķ�����Ϊ�� ��
A.��0��1��
B.[0��1]
C.�����ޣ�0���ȣ�1��+�ޣ�
D.�����ޣ�0]��[1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A�ǵ�λԲO��x��������Ľ��㣬P��Q��ԲO�����㣬OΪ����ԭ�㣬��AOP= ![]() ����AOQ=��������[0��
����AOQ=��������[0�� ![]() ]��
]��
��1����Q�� ![]() ��
�� ![]() ������cos������
������cos������ ![]() ����ֵ��
����ֵ��
��2���躯��f������=sin���� ![]()
![]() ������f��������ֵ��
������f��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��O�İ뾶��1����C��ֱ��AB���ӳ����ϣ�BC=1����P����O�ϰ�Բ�ϵ�һ�����㣬��PCΪ�����ȱ�������PCD���ҵ�D��Բ�ķֱ���PC��������
(1)����POB=�����Խ��ı���OPDC�����y��ʾΪ�������ĺ�����
(2)���ı���OPDC��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���������۹���AB��BC��ACΧ��ֱ�������Σ�����ֱ�DZ�BC=200m��б��AB=400m�����мס��ҡ�����λС���ѷֱ���AB��BC��AC�������Ϸ������λ�÷ֱ��Ϊ��D��E��F��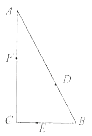
��1�����ס��Ҷ���ÿ����100m���ٶȴӵ�B�����ڸ��ԵĴ���ϱ��ߣ����������һ��ʱ��ͣ���ұȼ׳�2���ӳ��������ҳ���1���Ӻ����ʱ��������֮��ľ��룻
��2�����CEF=�ȣ��ұ�֮��ľ����Ǽ���֮������2�����ҡ�DEF= ![]() ���뽫����֮��ľ���y��ʾΪ�ȵĺ������������֮�����С���룮
���뽫����֮��ľ���y��ʾΪ�ȵĺ������������֮�����С���룮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com