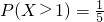练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    随机变量X服从正态分布N（μ，δ2），若X～（0，1），数学公式，则P（-1≤X＜0）=


    1. A.
      数学公式
    2. B.
      数学公式
    3. C.
      数学公式
    4. D.
      数学公式
    A
    分析：根据ξ～N（0，1），可得图象关于x=0对称，利用P（X＞1）=，即可求得结论．
    解答：根据正态分布N（0，1）的密度函数的图象的对称性可得，
    ∵ξ～N（0，1），∴图象关于x=0对称
    ∴P（-1≤X＜0）=P（0＜X＜≤1）=[1-2P（X＞1）]==
    故选A．
    点评：本题主要考查正态分布的图象，利用正态曲线的对称性是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某随机变量ξ服从正态分布，其概率密度函数为f(x)=
    1
    		8π
    e-
    x2
    8
    ，则ξ的期望和标准差分别是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    关于正态分布下列说法正确的是            

    ①一个随机变量如果是众多的互不相干的、不分主次的偶然因素之和，它就服从正态分布.

    ②正态曲线式频率折线图的极限状态

    ③任何正态分布的曲线下方，x轴上方总面积为1

    ④正态总体N(3,4)的标准差为4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    关于正态分布下列说法正确的是________
    ①一个随机变量如果是众多的互不相干的、不分主次的偶然因素之和，它就服从正态分布.
    ②正态曲线式频率折线图的极限状态
    ③任何正态分布的曲线下方，x轴上方总面积为1
    ④正态总体N(3,4)的标准差为4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某随机变量ξ服从正态分布，其概率密度函数为f(x)=
    1
    		8π
    e-
    x2
    8
    ，则ξ的期望和标准差分别是（　　）
    A．0和8B．0和4C．0和
    		2
    		D．0和2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列几个命题

    ①从匀速传递的产品生产流水线上，质检员每10分钟从某处抽取一件产品进行某项指标检测，这样的抽样是分层抽样。

    ②对于一组数据xi（i=1，2，…），如果将它们变换成xi+1(i=1，2，…，)，则变换后的数据平均数变了，而方差保持不变.

    ③在回归直线方程=0.1x+10中，当解释变量x每增加一个单位时，预报变量增加0.1个单位.

    ④某地气象局预报：5月9日本地降水概率为90%.结果这天一点雨都没下，这表明天气矛盾并不科学.

    ⑤如果一个随机变量是众多、互不相干的、不分主次的偶然因素作用结果之和，那么这个随机变量就服从或近似服从正态分布，

    其中正确命题的序号为           （把你认为所有正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案