
【题目】已知△ABC中, ![]() =λ
=λ ![]() (0<λ<1),cosC=
(0<λ<1),cosC= ![]() ,cos∠ADC=
,cos∠ADC= ![]() .
.
(1)若AC=5.BC=7,求AB的大小;
(2)若AC=7,BD=10,求△ABC的面积.
【答案】
(1)解:∵ ![]() ,∴D在边BC上,且不与B,C重合,如图所示,
,∴D在边BC上,且不与B,C重合,如图所示,
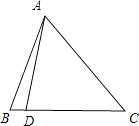
若AC=5,BC=7,∵ ![]() ;
;
∴在△ABC中由余弦定理得:
AB2=AC2+BC2﹣2ACBCcosC
= ![]()
=32;
∴ ![]() ;
;
(2)解:cosC= ![]() ,
, ![]() ;
;
∴ ![]() ;
;
∴sin∠DAC=sin[π﹣(C+∠ADC)]
=sin(C+∠ADC)
=sinCcos∠ADC+cosCsin∠ADC
= ![]()
= ![]() ;
;
又AC=7;
∴在△ACD中由正弦定理得: ![]() ;
;
即 ![]() ;
;
∴DC=5;
∴BC=BD+DC=15;
∴ ![]()
【解析】(1)在△ABC中, ![]() ,这样根据余弦定理即可求出AB2的值,从而求出AB的大小;(2)可由cosC和cos∠ADC的值求出sinC和sin∠ADC的值,从而由sin∠DAC=sin(C+∠ADC)及两角和的正弦公式即可求出sin∠DAC的值,这样在△ACD中,由正弦定理即可求出DC的大小,从而得出BC的大小,这样由三角形的面积公式即可求出△ABC的面积.
,这样根据余弦定理即可求出AB2的值,从而求出AB的大小;(2)可由cosC和cos∠ADC的值求出sinC和sin∠ADC的值,从而由sin∠DAC=sin(C+∠ADC)及两角和的正弦公式即可求出sin∠DAC的值,这样在△ACD中,由正弦定理即可求出DC的大小,从而得出BC的大小,这样由三角形的面积公式即可求出△ABC的面积.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(1)分别求甲队总得分为0分;2分的概率;
(2)求甲队得2分乙队得1分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1= ![]() ,an+1﹣1=an(an﹣1)(n∈N*)且Sn=
,an+1﹣1=an(an﹣1)(n∈N*)且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,则Sn的整数部分的所有可能值构成的集合是( )
,则Sn的整数部分的所有可能值构成的集合是( )
A.{0,1,2}
B.{0,1,2,3}
C.{1,2}
D.{0,2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知f(x+1)=x2+4x+1,求f(x)的解析式.
(2)已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9.求f(x).
(3)已知f(x)满足2f(x)+f ![]() =3x,求f(x).
=3x,求f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在(﹣∞,+∞)上的偶函数,且它在[0,+∞)上单调递增,若a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(﹣2),则a,b,c的大小关系是(从小到大排)
),c=f(﹣2),则a,b,c的大小关系是(从小到大排)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com