
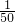 a(100+2x)(10-x)(0<x<10);(6分)
a(100+2x)(10-x)(0<x<10);(6分)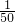 a(100+2x)(10-x)≥200a×10%×83.2%(8分)
a(100+2x)(10-x)≥200a×10%×83.2%(8分)

科目:高中数学 来源: 题型:解答题
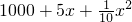 元,当出售这种产品x吨时,每吨价格是
元,当出售这种产品x吨时,每吨价格是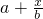 (a,b是常数)元,如果生产出来的这种产品能全部出售,那么当产量是150吨时,利润最大,并且这时每吨的价格是40元,求a,b的值.
(a,b是常数)元,如果生产出来的这种产品能全部出售,那么当产量是150吨时,利润最大,并且这时每吨的价格是40元,求a,b的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
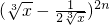 展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.
展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.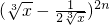 展开式中的所有的有理项.
展开式中的所有的有理项.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
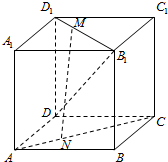 已知正方体ABCD-A1B1C1D1中,点M为线段D1B1上的动点,点N为线段AC上的动点,则与线段DB1相交且互相平分的线段MN有
已知正方体ABCD-A1B1C1D1中,点M为线段D1B1上的动点,点N为线段AC上的动点,则与线段DB1相交且互相平分的线段MN有查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com