练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    ．设二次函数的值域为，且，则的最大值为（   ）
    A．B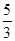．C．D．
    C
    根据f（1）≤4，求得4≤a+c≤8由题意可知，a＞0，△=0，从而求出ac=4，将所求式子中的4代换成ac，利用裂项法进行整理，进而利用函数的单调性求得u=的最大值．
    解：f（x）的值域为[0，+∞），故 

    又0≤f（1）≤4，即0≤a-4+c≤4，
    所以4≤a+c≤8
    u===
    由y=t-的单调性，umax=
    故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    已知，则函数的零点个数为（   ）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分13分） 已知函数，且对于任意实数，恒有.
    （1）求函数的解析式；
    （2）已知函数在区间上单调，求实数的取值范围；
    （3）若函数有2个零点？求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数的定义域为，值域为，那么满足条件的整数对共有                                         （   ）
    A．个B．个C．个D．个

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某公园准备建一个摩天轮，摩天轮的外围是一个周长为米的圆．在这个圆上安装座位，且每个座位和圆心处的支点都有一根直的钢管相连．经预算，摩天轮上的每个座位与支点相连的钢管的费用为元/根，且当两相邻的座位之间的圆弧长为米时，相邻两座位之间的钢管和其中一个座位的总费用为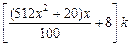元，假设座位等距离分布，且至少有四个座位，所有座位都视为点，且不考虑其他因素，记摩天轮的总造价为元.
    （Ⅰ）试写出关于的函数关系式，并写出定义域；
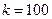    （Ⅱ）当米时，试确定座位的个数，使得总造价最低？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题


    设是定义在R上的奇函数，当x≤0时，=，则       .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某企业2010年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降。若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在末扣除技术资金的情况下，第n年（2011年为第一年）的利润为500（1+）万元（n为正整数）
    （1）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为万元，进行技术改造后的累计纯利润为万元（须扣除技术改造资金），求、的表达式；
    （2）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设，则的值为
    .          .          .         .  

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知实数成等比数列，且对函数，当时取到极大值，则等于（）
    A．         B．0            C．1           D．2

    查看答案和解析>>

    同步练习册答案