设函数f(x)=x2-2(-1)klnx(k∈N*),f′(x)表示f(x)I的导函数.
(1)求函数y=f(x)的单调增区间;
(2)当it为偶数时,数列{an}满足:a1=1,anf′(an)=an+12-3.证明:数列{an2}中的任意三项不能构成等差数列;
(3)当k为奇数时,证明:对任意正整数都有[f′(x)]n-2n-1f′(xn)≥2n(2n-2)成立.
【答案】
分析:(1)先求函数f(x)的导数,f′(x),再对k进行奇偶数讨论:1°当k 为奇数时,f′(x)=

;2°当k 为偶数时,f′(x)=

;最后综合即可;
(2)当k 为偶数时,由(1)知f′(x)=

,由条件得{a
n 2+1}是一个公比为2的等比数列,从而得到a
n2=2
n-1,最后利用反证法进行证明即可;
(3)当k为奇数时,f′(x)=2(x+
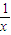
),欲证原不等式成立,即证:(x+

)
n-(x
n+

)≥2
n-2,由二项式定理得,即证:C
n1x
n-2+C
n2x
n-4+…+C
n 2-n x
2-n≥2
n-2,
设Sn=C
n1x
n-2+C
n2x
n-4+…+C
n 2-nx
2-n,利用倒序相加法即可证得.
解答:解:(1)函数f(x)的定义域为(0,+∞),又f′(x)=2x-2(-1)
k
=
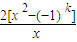
,
1°当k 为奇数时,f′(x)=

,∵x∈(0,+∞),∴f′(x)>0恒成立;
2°当k 为偶数时,f′(x)=

,∵∴x+1>0,f′(x)>0得x>1,即f(x)的单调增区间为(1,+∞),
综上所述,当k 为奇数时,f(x)的单调增区间为(0,+∞),当k 为偶数时,即f(x)的单调增区间为(1,+∞),
(2)当k 为偶数时,由(1)知f′(x)=

,∴f′(an)=

,
由条件得:2(a
n2-1)=a
n+12-3,故有:a
n+12+1=2(a
n2+1),
∴{a
n 2+1}是一个公比为2的等比数列,∴a
n2=2
n-1,
假设数列{a
n2}中的存在三项a
r2,s
2,a
t2,能构成等差数列
不妨设r<s<t,则2a
s 2=a
r 2+a
t 2,
即2(2
s-1)=2
r-1+2
t-1,∴2
s-r+1=1+2
t-r,
又s-r+1>0,t-r>0,∴2
s-r+1为偶数,1+2
t-r为奇数,故假设不成立,
因此,数列{a
n2}中的任意三项不能构成等差数列;
(3)当k为奇数时,f′(x)=2(x+

),即证:(x+
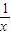
)
n-(x
n+

)≥2
n-2,
由二项式定理得,即证:C
n1x
n-2+C
n2x
n-4+…+C
n 2-n x
2-n≥2
n-2,
设Sn=C
n1x
n-2+C
n2x
n-4+…+C
n 2-nx
2-n,
Sn=C
n2-nx
2-n+…+C
n2x
n-4+C
n1x
n-2,
两式相加得:
2Sn=C
n1(x
n-2+x
2-n)+C
n2(x
n-4+x
4-n)+…+C
nn-1(x
n-2+x
2-n)≥2(C
n1+C
n2+…+C
n2-n)=2(2
n-1),
∴Sn≥2
n-2,
即原不等式成立.
点评:本小题主要考查等差关系的确定、利用导数研究函数的单调性、用数学归纳法证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

 ;2°当k 为偶数时,f′(x)=
;2°当k 为偶数时,f′(x)= ;最后综合即可;
;最后综合即可; ,由条件得{an 2+1}是一个公比为2的等比数列,从而得到an2=2n-1,最后利用反证法进行证明即可;
,由条件得{an 2+1}是一个公比为2的等比数列,从而得到an2=2n-1,最后利用反证法进行证明即可;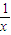 ),欲证原不等式成立,即证:(x+
),欲证原不等式成立,即证:(x+ )n-(xn+
)n-(xn+ )≥2n-2,由二项式定理得,即证:Cn1xn-2+Cn2xn-4+…+Cn 2-n x 2-n≥2n-2,
)≥2n-2,由二项式定理得,即证:Cn1xn-2+Cn2xn-4+…+Cn 2-n x 2-n≥2n-2, =
=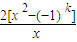 ,
, ,∵x∈(0,+∞),∴f′(x)>0恒成立;
,∵x∈(0,+∞),∴f′(x)>0恒成立; ,∵∴x+1>0,f′(x)>0得x>1,即f(x)的单调增区间为(1,+∞),
,∵∴x+1>0,f′(x)>0得x>1,即f(x)的单调增区间为(1,+∞), ,∴f′(an)=
,∴f′(an)= ,
, ),即证:(x+
),即证:(x+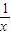 )n-(xn+
)n-(xn+ )≥2n-2,
)≥2n-2,

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案