
【题目】如图,在四棱锥PABCD中,底面ABCD是矩形,点E在棱PC上![]() 异于点P,
异于点P,![]() ,平面ABE与棱PD交于点F
,平面ABE与棱PD交于点F

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求证:平面
,求证:平面![]() 平面ABCD.
平面ABCD.
【答案】(1)见解析(2)见解析
【解析】
分析:(1)推导出AB∥CD,从而AB∥平面PDC,由此能证明AB∥EF.(2)结合(1)可证AB⊥AF,AB⊥平面PAD,从而得平面PAD⊥平面ABCD.
证明:(1) 因为四边形ABCD是矩形,
所以AB//CD.
又AB平面PDC,CD平面PDC,
所以AB//平面PDC,
又因为AB平面ABE,平面ABE∩平面PDC=EF,
所以AB//EF.
(2) 因为四边形ABCD是矩形,
所以AB⊥AD.
因为AF⊥EF,(1)中已证AB//EF,
所以AB⊥AF,
又AB⊥AD,
由点E在棱PC上(异于点C),所以F点异于点D,
所以AF∩AD=A,
AF,AD平面PAD,
所以AB⊥平面PAD,
又AB平面ABCD,
所以平面PAD⊥平面ABCD.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】某科研小组有20个不同的科研项目,每年至少完成一项。有下列两种完成所有科研项目的计划:
A计划:第一年完成5项,从第一年开始,每年完成的项目不得少于次年,直到全部完成为止;
B计划:第一年完成项数不限,从第一年开始,每年完成的项目不得少于次年,恰好5年完成所有项目。
那么,按照A计划和B计划所安排的科研项目不同完成顺序的方案数量
A. 按照A计划完成的方案数量多
B. 按照B计划完成的方案数量多
C. 按照两个计划完成的方案数量一样多
D. 无法判断哪一种计划的方案数量多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)记![]() 的导函数为
的导函数为![]() ,若不等式
,若不等式![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若
的导函数,若![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《红海行动》是一部现代海军题材影片,该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事.撤侨过程中,海军舰长要求队员们依次完成六项任务,并对任务的顺序提出了如下要求:重点任务![]() 必须排在前三位,且任务
必须排在前三位,且任务![]() 、
、![]() 必须排在一起,则这六项任务的不同安排方案共有_____种.
必须排在一起,则这六项任务的不同安排方案共有_____种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查微信用户每天使用微信的时间,某经销化妆品的店家在一广场随机采访男性、女性用户各50名,将男性、女性平均每天使用微信的时间(单位:![]() )分成5组:
)分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
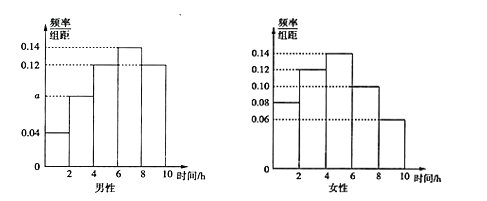
(1)根据男性的频率分布直方图,求![]() 的值;
的值;
(2)①若每天玩微信超过![]() 的用户称为“微信控”,否则称为“非微信控”,根据男性,女性频率分布直方图完成下面
的用户称为“微信控”,否则称为“非微信控”,根据男性,女性频率分布直方图完成下面![]() 列联表(不用写计算过程)
列联表(不用写计算过程)
微信控 | 非微信 | 总计 | |
男性 | |||
女性 | |||
总计 | 100 |
②判断是否有90%的把握认为“微信控”与性别有关?说明你的理由.(下面独立性检验的临界值表供参考)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意正整数
,且对任意正整数![]() ,
,![]() 都为
都为![]() 中等于
中等于![]() 的项的个数,则称数列
的项的个数,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)请列举出三个![]() 数列,每个
数列,每个![]() 数列只写出其前5项;
数列只写出其前5项;
(2)若数列![]() 为一个
为一个![]() 数列,证明:
数列,证明:![]() ,都有
,都有![]() ;
;
(3)若数列![]() 为一个
为一个![]() 数列,求集合
数列,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com