
 千米的C,D两点分别测得∠ACB=75°,∠DCB=45°,∠ADC=30°,∠ADB=45°,(A,B,C,D在同一平面内),求展馆A,B之间的距离.
千米的C,D两点分别测得∠ACB=75°,∠DCB=45°,∠ADC=30°,∠ADB=45°,(A,B,C,D在同一平面内),求展馆A,B之间的距离.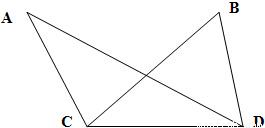
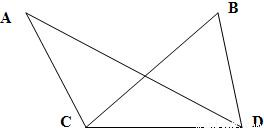 解:在△ACD中,∠DAC=180°-∠ACB-∠BCD-∠ADC=30°,∠ADC=30°,
解:在△ACD中,∠DAC=180°-∠ACB-∠BCD-∠ADC=30°,∠ADC=30°,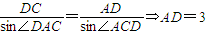
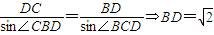 ,
,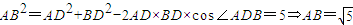 .
.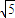 千米.
千米.

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 为迎接2010年上海世博会,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为5cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
为迎接2010年上海世博会,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为5cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.查看答案和解析>>
科目:高中数学 来源: 题型:
 某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com