
【题目】已知点P(﹣1, ![]() )是椭圆E:
)是椭圆E: ![]() =1(a>b>0)上一点,F1 , F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
=1(a>b>0)上一点,F1 , F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(1)求椭圆E的方程;
(2)设A,B是椭圆E上两个动点,满足: ![]() (0<λ<4,且λ≠2),求直线AB的斜率.
(0<λ<4,且λ≠2),求直线AB的斜率.
(3)在(2)的条件下,当△PAB面积取得最大值时,求λ的值.
【答案】
(1)
解:∵PF1⊥x轴,∴F1(﹣1,0),c=1,F2(1,0),
∴|PF2|= ![]() =
= ![]() ,∴2a=|PF1|+|PF2|=4,∴a=2,∴b2=3,
,∴2a=|PF1|+|PF2|=4,∴a=2,∴b2=3,
∴椭圆E的方程为: ![]()
(2)
证明:设A(x1,y1)、B(x2,y2),
由 ![]() (0<λ<4,且λ≠2),得(x1+1,y1﹣
(0<λ<4,且λ≠2),得(x1+1,y1﹣ ![]() )+(x2+1,y2﹣
)+(x2+1,y2﹣ ![]() )=λ(1,﹣
)=λ(1,﹣ ![]() ),
),
∴x1+x2=λ﹣2,y1+y2= ![]() (2﹣λ)…①
(2﹣λ)…①
又 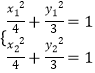 ,两式相减得3(x1+x2)(x1﹣x2)+4(y1+y2)(y1﹣y2)=0…..②
,两式相减得3(x1+x2)(x1﹣x2)+4(y1+y2)(y1﹣y2)=0…..②
以①式代入可得AB的斜率k= ![]() =
= ![]()
(3)
解:设直线AB的方程为y= ![]() x+t,与3x2+4y2=12联立消去y并整理得 x2+tx+t2﹣3=0,△=3(4﹣t2),
x+t,与3x2+4y2=12联立消去y并整理得 x2+tx+t2﹣3=0,△=3(4﹣t2),
|AB|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]() ×
× ![]() =
= ![]() ,
,
点P到直线AB的距离为d= ![]() ,
,
△PAB的面积为S= ![]() |AB|×d=
|AB|×d= ![]() ×
× ![]() |t﹣2|,
|t﹣2|,
设f(t)=S2=﹣ ![]() (t4﹣4t3+16t﹣16)(﹣2<t<2),
(t4﹣4t3+16t﹣16)(﹣2<t<2),
f′(t)=﹣3(t3﹣3t2+4)=﹣3(t+1)(t﹣2)2,由f′(t)=0及﹣2<t<2得t=﹣1.
当t∈(﹣2,﹣1)时,f′(t)>0,
当t∈(﹣1,2)时,f′(t)<0,f(t)=﹣1时取得最大值 ![]() ,
,
所以S的最大值为 ![]() .
.
此时x1+x2=﹣t=1=λ﹣2,λ=3.
【解析】(1)由PF1⊥x轴,求出2a=|PF1|+|PF2|=4,由此能求出椭圆E的方程.(2)设A(x1 , y1)、B(x2 , y2),由 ![]() (0<λ<4,且λ≠2),得x1+x2=λ﹣2,y1+y2=
(0<λ<4,且λ≠2),得x1+x2=λ﹣2,y1+y2= ![]() (2﹣λ),再由3(x1+x2)(x1﹣x2)+4(y1+y2)(y1﹣y2)=0,由此能求出AB的斜率.(3)设直线AB的方程为y=
(2﹣λ),再由3(x1+x2)(x1﹣x2)+4(y1+y2)(y1﹣y2)=0,由此能求出AB的斜率.(3)设直线AB的方程为y= ![]() x+t,与3x2+4y2=12联立得 x2+tx+t2﹣3=0,由此利用根的判别式、弦长公式、点到直线距离公式、三角形面积公式,求出△PAB的面积为S=
x+t,与3x2+4y2=12联立得 x2+tx+t2﹣3=0,由此利用根的判别式、弦长公式、点到直线距离公式、三角形面积公式,求出△PAB的面积为S= ![]() ×
× ![]() |t﹣2|,设f(t)=S2=﹣
|t﹣2|,设f(t)=S2=﹣ ![]() (t4﹣4t3+16t﹣16)(﹣2<t<2),求出f′(t)=﹣3(t+1)(t﹣2)2 , 由f′(t)=0及﹣2<t<2得t=﹣1.由此能求出结果.
(t4﹣4t3+16t﹣16)(﹣2<t<2),求出f′(t)=﹣3(t+1)(t﹣2)2 , 由f′(t)=0及﹣2<t<2得t=﹣1.由此能求出结果.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),x0+ ![]() >3;命题q:x∈(2,+∞),x2>2x , 则下列命题为真的是( )
>3;命题q:x∈(2,+∞),x2>2x , 则下列命题为真的是( )
A.p∧(¬q)
B.(¬p)∧q
C.p∧q
D.(¬p)∨q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a2lnx+ax(a≠0),g(x)= ![]() 2tdt,F(x)=g(x)﹣f(x).
2tdt,F(x)=g(x)﹣f(x).
(1)试讨论F(x)的单调性;
(2)当a>0时,﹣e2≤F(x)≤1﹣e在x∈[1,e]恒成立,求实数a的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在队内羽毛球选拔赛中,选手M与B1 , B2 , B3三位选手分别进行一场对抗赛,按以往多次比赛的统计,M获胜的概率分别为 ![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若M至少获胜两场的概率大于 ![]() ,则M入选下一轮,否则不予入选,问M是否会入选下一轮?
,则M入选下一轮,否则不予入选,问M是否会入选下一轮?
(2)求M获胜场数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1 , ∠BAA1=∠BAC=60°,点O是线段AB的中点. (Ⅰ)证明:BC1∥平面OA1C;
(Ⅱ)若AB=2,A1C= ![]() ,求二面角A﹣BC﹣A1的余弦值.
,求二面角A﹣BC﹣A1的余弦值.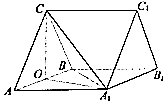
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com