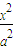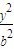练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆+=1，（a＞b＞0）的长轴为AB，以AB为底边作椭圆的内接等腰梯形ABCD，求此等腰梯形面积的最大值．
    【答案】分析：先设C（acosφ，bsinφ）进而可得四边形ABCD 的面积的表达式整理得4absincos3，进而根据sincos3的范围求得答案．
    解答：解：设C（acosφ，bsinφ），则四边形ABCD 的面积=absinφ+abcosφsinφ
    =absinφ（1+cosφ）=4absincos3
    因为sin2×cos6
    =×3sin2×cos2×cos2×cos2
    ≤×（）4=．
    所以sincos≤．
    所以则四边形ABCD的面积的最大值为：．
    点评：本题主要考查了椭圆的简单性质．本题利用了椭圆的参数方程通过三角函数的性质来解决问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆=1内一点A(1，1)，则过点A且被该点平分的弦所在直线的方程是_________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （文）已知椭圆数学公式=1内一点A（1，1），则过点A且被该点平分的弦所在直线的方程是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆=1按向量a=(t-3,t2)(t∈R)平移后得到曲线E,设曲线E的右焦点为P.

    (1)求P点轨迹C的方程;

    (2)A、B为曲线C上的两点,F(0,),且(m∈R),求∠AOB(O为坐标原点)的最大值.

    (文)已知函数f(x)=xn+1(n∈N*,x≠0).

    (1)讨论函数f(x)图象的对称性,并指出其一条对称轴或一个对称中心;

    (2)令an=f′(x),求数列{an}的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源：2007年天津市汉沽一中高三第一次调研数学试卷（解析版） 题型：解答题

    （文）已知椭圆=1内一点A（1，1），则过点A且被该点平分的弦所在直线的方程是    ．

    查看答案和解析>>

    同步练习册答案