
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】某篮球队有![]() 名队员,其中有
名队员,其中有![]() 名队员打前锋,有
名队员打前锋,有![]() 名队员打后卫,甲、乙两名队员既能打前锋又能打后卫.若出场阵容为
名队员打后卫,甲、乙两名队员既能打前锋又能打后卫.若出场阵容为![]() 名前锋,
名前锋,![]() 名后卫,则不同的出场阵容共有______种.
名后卫,则不同的出场阵容共有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂抽取了一台设备![]() 在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.

(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)根据长期生产经验,可以认为这台设备在正常状态下生产的产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为样本平均值,
近似为样本平均值,![]() 近似为样本方差
近似为样本方差![]() .任取一个产品,记其质量指标值为
.任取一个产品,记其质量指标值为![]() .若
.若![]() ,则认为该产品为一等品;
,则认为该产品为一等品;![]() ,则认为该产品为二等品;若
,则认为该产品为二等品;若![]() ,则认为该产品为不合格品.已知设备
,则认为该产品为不合格品.已知设备![]() 正常状态下每天生产这种产品1000个.
正常状态下每天生产这种产品1000个.
(i)用样本估计总体,问该工厂一天生产的产品中不合格品是否超过![]() ?
?
(ii)某公司向该工厂推出以旧换新活动,补足50万元即可用设备![]() 换得生产相同产品的改进设备
换得生产相同产品的改进设备![]() .经测试,设备
.经测试,设备![]() 正常状态下每天生产产品1200个,生产的产品为一等品的概率是
正常状态下每天生产产品1200个,生产的产品为一等品的概率是![]() ,二等品的概率是
,二等品的概率是![]() ,不合格品的概率是
,不合格品的概率是![]() .若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备
.若工厂生产一个一等品可获得利润50元,生产一个二等品可获得利润30元,生产一个不合格品亏损40元,试为工厂做出决策,是否需要换购设备![]() ?
?
参考数据:①![]() ;②
;②![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1左右焦点为F1,F2直线(
1左右焦点为F1,F2直线(![]() 1)x
1)x![]() y
y![]() 0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
0与该椭圆有一个公共点在y轴上,另一个公共点的坐标为(m,1).
(1)求椭圆C的方程;
(2)设P为椭圆C上任一点,过焦点F1,F2的弦分别为PM,PN,设![]() λ1
λ1![]() λ2
λ2![]() ,求λ1+λ2的值.
,求λ1+λ2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
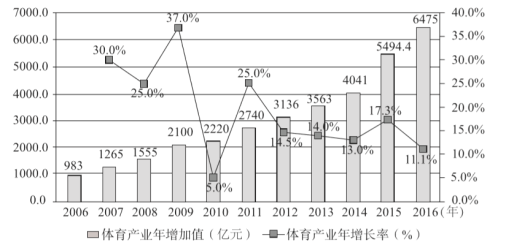
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,点A,B分别是椭圆E的左顶点和上顶点,直线AB与圆C:x2+y2=c2相离,其中c是椭圆的半焦距,P是直线AB上一动点,过点P作圆C的两条切线,切点分别为M,N,若存在点P使得△PMN是等腰直角三角形,则椭圆离心率平方e2的取值范围是_____.
,点A,B分别是椭圆E的左顶点和上顶点,直线AB与圆C:x2+y2=c2相离,其中c是椭圆的半焦距,P是直线AB上一动点,过点P作圆C的两条切线,切点分别为M,N,若存在点P使得△PMN是等腰直角三角形,则椭圆离心率平方e2的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为![]() 元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
序号 | 分组 | 频数(天) | 频率 |
1 |
|
| 0.16 |
2 |
| 12 |
|
3 |
|
| 0.3 |
4 |
|
|
|
5 |
| 5 | 0.1 |
合计 | 50 | 1 | |
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 关于日需求量
关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com