
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
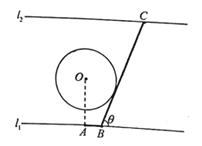
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AOB是一块半径为r的扇形空地,![]() .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若![]() ,设
,设![]()
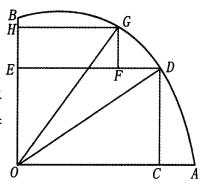
(Ⅰ)记活动场地与停车场占地总面积为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅱ)当![]() 为何值时,可使活动场地与停车场占地总面积最大.
为何值时,可使活动场地与停车场占地总面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈[-1,1],函数
,x∈[-1,1],函数![]() ,a∈R的最小值为h(a).
,a∈R的最小值为h(a).
(1)求h(a)的解析式;
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() 且
且![]() 数列
数列![]() 满足
满足![]() 且对任意正整数
且对任意正整数![]() 都有
都有![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式.
的通项公式.
(2)证明数列![]() 为等差数列.
为等差数列.
(3)令![]() 问是否存在正整数
问是否存在正整数![]() 使得
使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,
中,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
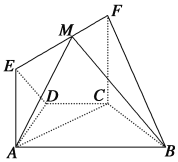
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com