
若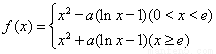 ,其中
,其中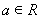 .
.
(1)当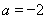 时,求函数
时,求函数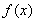 在区间
在区间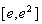 上的最大值;
上的最大值;
(2)当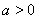 时,若
时,若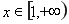 ,
,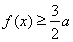 恒成立,求
恒成立,求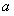 的取值范围.
的取值范围.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
某商店储存的50个灯泡中,甲厂生产的灯泡占60%,乙厂生产的灯泡占40%,甲厂生产的灯泡的一等品率是90%,乙厂生产的灯泡的一等品率是80%.
(1)若从这50个灯泡中随机抽取出1个灯泡(每个灯泡被取出的机会均等),则它是甲厂生产的一等品的概率是多少?
(2)若从这50个灯泡中随机抽取出2个灯泡(每个灯泡被取出的机会均等),这2个灯泡中是甲厂生产的一等品的个数记为ξ,求E(ξ)的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
已知☉O1和☉O2的极坐标方程分别是ρ=2cosθ和ρ=2asinθ(a是非零常数).
(1)将两圆的极坐标方程化为直角坐标方程.
(2)若两圆的圆心距为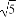 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
设函数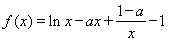 .
.
(Ⅰ)当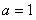 时,求曲线
时,求曲线 在
在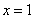 处的切线方程;
处的切线方程;
(Ⅱ)当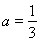 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数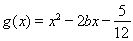 ,若对于
,若对于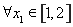 ,
,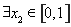 ,使
,使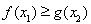 成立,求实数
成立,求实数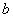 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
设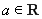 ,函数
,函数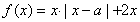 .
.
(1)若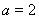 ,求函数
,求函数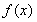 在区间
在区间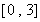 上的最大值;
上的最大值;
(2)若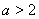 ,写出函数
,写出函数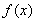 的单调区间(不必证明);
的单调区间(不必证明);
(3)若存在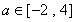 ,使得关于
,使得关于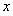 的方程
的方程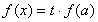 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数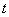 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知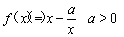 ,
,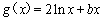 ,且直线
,且直线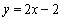 与曲线
与曲线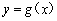 相切.
相切.
(1)若对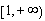 内的一切实数
内的一切实数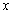 ,不等式
,不等式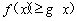 恒成立,求实数
恒成立,求实数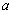 的取值范围;
的取值范围;
(2)当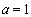 时,求最大的正整数
时,求最大的正整数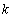 ,使得对
,使得对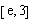 (
(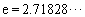 是自然对数的底数)内的任意
是自然对数的底数)内的任意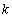 个实数
个实数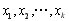 都有
都有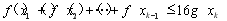 成立;
成立;
(3)求证: .
.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:填空题
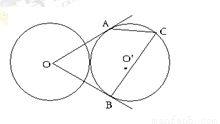
如图,两个等圆⊙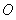 与⊙
与⊙ 外切,过
外切,过 作⊙
作⊙ 的两条切线
的两条切线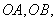
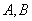 是切点,点
是切点,点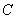 在圆
在圆 上且不与点
上且不与点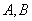 重合,则
重合,则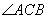 = .
= .
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
已知函数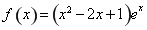 (其中
(其中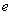 为自然对数的底数).
为自然对数的底数).
(1)求函数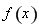 的单调区间;
的单调区间;
(2)定义:若函数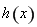 在区间
在区间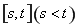 上的取值范围为
上的取值范围为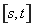 ,则称区间
,则称区间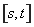 为函数
为函数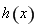 的“域同区间”.试问函数
的“域同区间”.试问函数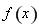 在
在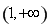 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com