
ЁОЬтФПЁПШчЭМвЛПщГЄЗНаЮЧјгђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдкБп
ЃЌдкБп![]() ЕФжаЕу
ЕФжаЕу![]() ДІгавЛИіПЩзЊЖЏЕФЬНееЕЦЃЌЦфееЩфНЧ
ДІгавЛИіПЩзЊЖЏЕФЬНееЕЦЃЌЦфееЩфНЧ![]() ЪМжеЮЊ
ЪМжеЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌЬНееЕЦееЩфдкГЄЗНаЮ
ЃЌЬНееЕЦееЩфдкГЄЗНаЮ![]() ФкВПЧјгђЕФУцЛ§ЮЊ
ФкВПЧјгђЕФУцЛ§ЮЊ![]() .
.
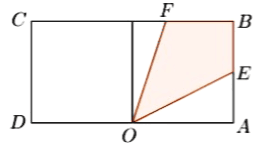
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШєЬНееЕЦУП9Зжжга§зЊЁАвЛИіРДЛиЁБЃЈ![]() зд
зд![]() зЊЕН
зЊЕН![]() ЃЌдйЛиЕН
ЃЌдйЛиЕН![]() ЃЌГЦЁАвЛИіРДЛиЁБЃЌКіТд
ЃЌГЦЁАвЛИіРДЛиЁБЃЌКіТд![]() дк
дк![]() МА
МА![]() ДІЫљгУЕФЪБМфЃЉЃЌЧвзЊЖЏЕФНЧЫйЖШДѓаЁвЛЖЈЃЌЩш
ДІЫљгУЕФЪБМфЃЉЃЌЧвзЊЖЏЕФНЧЫйЖШДѓаЁвЛЖЈЃЌЩш![]() БпЩЯгавЛЕу
БпЩЯгавЛЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() дкЁАвЛИіРДЛиЁБжаБЛееЕНЕФЪБМф.
дкЁАвЛИіРДЛиЁБжаБЛееЕНЕФЪБМф.
ЁОД№АИЁП(1)МћНтЮі;(2)![]() ;(3)2Зжжг.
;(3)2Зжжг.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтНсКЯШ§НЧКЏЪ§ЕФаджЪПЩЕУЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНсКЯ(1)жаКЏЪ§ЕФНтЮіЪНКЭШ§НЧКЏЪ§ЕФаджЪПЩЕУЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉНсКЯЪЕМЪЮЪЬтКЭШ§НЧКЏЪ§ЕФаджЪМЦЫуПЩЕУЕу![]() БЛееЕНЕФЪБМфЮЊ
БЛееЕНЕФЪБМфЮЊ![]() Зжжг.
Зжжг.
ЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() дк
дк![]() ЩЯ
ЩЯ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЁЂ
ЁЂ![]() ЖМдк
ЖМдк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
гЩгк![]() ЃЌЫљвдЕБ
ЃЌЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЁАвЛИіРДЛиЁБжаЃЌ![]() ЙВзЊЖЏСЫ
ЙВзЊЖЏСЫ![]() ЃЌ
ЃЌ
ЦфжаЕу![]() БЛееЕНЪБЃЌ
БЛееЕНЪБЃЌ![]() ЙВзЊЖЏСЫ
ЙВзЊЖЏСЫ![]() ЃЌ
ЃЌ
Еу![]() БЛееЕНЕФЪБМфЮЊ
БЛееЕНЕФЪБМфЮЊ![]() Зжжг.
Зжжг.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
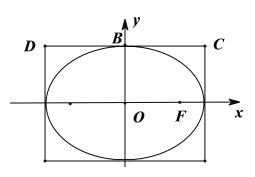
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШєЧњЯп![]() дк
дк![]() ДІЕФЧаЯпЕФаБТЪЮЊ2ЃЌЧѓКЏЪ§
ДІЕФЧаЯпЕФаБТЪЮЊ2ЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯгаСуЕуЃЌЧѓЪЕЪ§
ЩЯгаСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.ЃЈ
ЕФШЁжЕЗЖЮЇ.ЃЈ![]() ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌ
ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
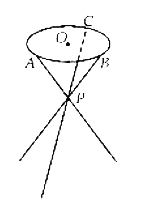
ЁОЬтФПЁПШчЭМЃЌаЁЕЪЕЪУцЮЊдВаЮЃЌЕЪНХЮЊШ§ИљЯИИжЙм.ПМТЧЕНИжЙмЕФЪмСІЕШвђЫиЃЌЩшМЦЕФаЁЕЪгІТњзуЃКШ§ИљЯИИжЙмЯрНЛДІЕФНкЕу![]() гыЕЪУцдВаЮЕФдВаФ
гыЕЪУцдВаЮЕФдВаФ![]() ЕФСЌЯпДЙжБгкЕЪУцКЭЕиУцЃЌЧв
ЕФСЌЯпДЙжБгкЕЪУцКЭЕиУцЃЌЧв![]() ЗжЯИИжЙмЩЯЯТСНЖЮЕФБШжЕЮЊ
ЗжЯИИжЙмЩЯЯТСНЖЮЕФБШжЕЮЊ![]() ЃЌШ§жЛЕЪНХгыЕиУцЫљГЩЕФНЧОљЮЊ
ЃЌШ§жЛЕЪНХгыЕиУцЫљГЩЕФНЧОљЮЊ![]() .Шє
.Шє![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЪЧЕЪУцдВжмЕФШ§ЕШЗжЕуЃЌ
ЪЧЕЪУцдВжмЕФШ§ЕШЗжЕуЃЌ![]() РхУзЃЌЧѓЕЪзгЕФИпЖШ
РхУзЃЌЧѓЕЪзгЕФИпЖШ![]() МАШ§ИљЯИИжЙмЕФзмГЄЖШ(ОЋШЗЕН
МАШ§ИљЯИИжЙмЕФзмГЄЖШ(ОЋШЗЕН![]() ).
).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіШ§НЧаЮЪ§БэАДШчЯТЗНЪНЙЙГЩЃЈШчЭМЃКЦфжаЯюЪ§![]() ЃЉЃКЕквЛааЪЧвд4ЮЊЪзЯюЃЌ4ЮЊЙЋВюЕФЕШВюЪ§СаЃЌДгЕкЖўааЦ№ЃЌУПвЛИіЪ§ЪЧЦфМчЩЯСНИіЪ§ЕФКЭЃЌР§ШчЃК
ЃЉЃКЕквЛааЪЧвд4ЮЊЪзЯюЃЌ4ЮЊЙЋВюЕФЕШВюЪ§СаЃЌДгЕкЖўааЦ№ЃЌУПвЛИіЪ§ЪЧЦфМчЩЯСНИіЪ§ЕФКЭЃЌР§ШчЃК![]() ЃЛ
ЃЛ![]() ЮЊЪ§БэжаЕк
ЮЊЪ§БэжаЕк![]() ааЕФЕк
ааЕФЕк![]() ИіЪ§.
ИіЪ§.
![]()
![]() Ё
Ё![]()
![]()
![]()
![]() Ё
Ё![]()
![]() Ё
Ё![]()
ЁЁ
![]()
ЃЈ1ЃЉЧѓЕк2ааКЭЕк3ааЕФЭЈЯюЙЋЪН![]() КЭ
КЭ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжЄУїЃКЪ§БэжаГ§зюКѓ2ааЭтУПвЛааЕФЪ§ЖМвРДЮГЩЕШВюЪ§СаЃЌВЂЧѓ![]() Йигк
Йигк![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ3ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЪдЧѓвЛИіЕШБШЪ§Са
ЃЌЪдЧѓвЛИіЕШБШЪ§Са![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЧвЖдгкШЮвтЕФ
ЃЌЧвЖдгкШЮвтЕФ![]() ЃЌОљДцдкЪЕЪ§
ЃЌОљДцдкЪЕЪ§![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЖМга
ЪБЃЌЖМга![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЩњЬЌдАНЋвЛШ§НЧаЮЕиПщABCЕФвЛНЧAPQПЊБйЮЊЫЎЙћдАжжжВЬвЪїЃЌвбжЊНЧAЮЊ![]() ЕФГЄЖШОљДѓгк200УзЃЌЯждкБпНчAPЃЌAQДІНЈЮЇЧНЃЌдкPQДІЮЇжёРщАЪ.
ЕФГЄЖШОљДѓгк200УзЃЌЯждкБпНчAPЃЌAQДІНЈЮЇЧНЃЌдкPQДІЮЇжёРщАЪ.

ЃЈ1ЃЉШєЮЇЧНAP,AQзмГЄЖШЮЊ200УзЃЌШчКЮЮЇПЩЪЙЕУШ§НЧаЮЕиПщAPQЕФУцЛ§зюДѓЃП
ЃЈ2ЃЉвбжЊAPЖЮЮЇЧНИп1УзЃЌAQЖЮЮЇЧНИп1.5УзЃЌдьМлОљЮЊУПЦНЗНУз100дЊ.ШєЮЇЮЇЧНгУСЫ20000дЊЃЌЮЪШчКЮЮЇПЩЪЙжёРщАЪгУСЯзюЪЁЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШ§РтжљABCЉA1B1C1ЕФВрУцAA1B1BЪЧСтаЮЃЌВрУцAA1C1CЪЧОиаЮЃЌЦНУцAA1C1CЁЭЦНУцAA1B1BЃЌЁЯBAA1![]() ЃЌAA1=2AC=2ЃЌOЮЊAA1ЕФжаЕу.
ЃЌAA1=2AC=2ЃЌOЮЊAA1ЕФжаЕу.
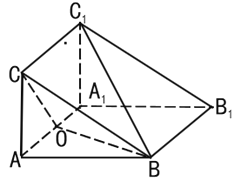
ЃЈ1ЃЉЧѓжЄ:OCЁЭBC1ЃЛ
ЃЈ2ЃЉЧѓЕуC1ЕНЦНУцABCЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPABCжаЃЌPAЁЭЕзУцABCDЃЌADЁЮBCЃЌAB=AD=AC=3ЃЌPA=BC=4ЃЌMЮЊЯпЖЮADЩЯвЛЕуЃЌAM=2MDЃЌNЮЊPCЕФжаЕу.

ЃЈЂёЃЉжЄУїMNЁЮЦНУцPAB;
ЃЈЂђЃЉЧѓжБЯпANгыЦНУцPMNЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
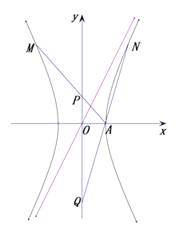
ЁОЬтФПЁПвбжЊжБЯп![]() ЪЧЫЋЧњЯп
ЪЧЫЋЧњЯп![]() ЕФвЛЬѕНЅНќЯпЃЌЕу
ЕФвЛЬѕНЅНќЯпЃЌЕу![]()
![]() ЖМдкЫЋЧњЯп
ЖМдкЫЋЧњЯп![]() ЩЯЃЌжБЯп
ЩЯЃЌжБЯп![]() гы
гы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЩшзјБъдЕуЮЊ
ЃЌЩшзјБъдЕуЮЊ![]() .
.
ЃЈ1ЃЉЧѓЫЋЧњЯп![]() ЕФЗНГЬЃЌВЂЧѓГіЕу
ЕФЗНГЬЃЌВЂЧѓГіЕу![]() ЕФзјБъЃЈгУ
ЕФзјБъЃЈгУ![]() БэЪОЃЉЃЛ
БэЪОЃЉЃЛ
ЃЈ2ЃЉЩшЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕуЮЊ
жсЕФЖдГЦЕуЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() .ЮЪЃКдк
.ЮЪЃКдк![]() жсЩЯЪЧЗёДцдкЖЈЕу
жсЩЯЪЧЗёДцдкЖЈЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉШєЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЪдЧѓжБЯп
ЃЌЪдЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЭждВ![]() ЃК
ЃК![]() ЃЈ
ЃЈ![]() ЃЉЕФгвНЙЕуЮЊ
ЃЉЕФгвНЙЕуЮЊ![]() ЃЌЖЬжсЕФвЛИіЖЫЕу
ЃЌЖЬжсЕФвЛИіЖЫЕу![]() ЕН
ЕН![]() ЕФОрРыЕШгкНЙОрЃЎ
ЕФОрРыЕШгкНЙОрЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЩш![]() ЁЂ
ЁЂ![]() ЪЧЫФЬѕжБЯп
ЪЧЫФЬѕжБЯп![]() ЃЌ
ЃЌ![]() ЫљЮЇГЩЕФОиаЮдкЕквЛЁЂЕкЖўЯѓЯоЕФСНИіЖЅЕуЃЌ
ЫљЮЇГЩЕФОиаЮдкЕквЛЁЂЕкЖўЯѓЯоЕФСНИіЖЅЕуЃЌ![]() ЪЧЭждВ
ЪЧЭждВ![]() ЩЯШЮвтвЛЕуЃЌШє
ЩЯШЮвтвЛЕуЃЌШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
ЃЈ3ЃЉЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгкВЛЭЌЕФСНЕу
НЛгкВЛЭЌЕФСНЕу![]() ЁЂ
ЁЂ![]() ЃЌЧвТњзуЁї
ЃЌЧвТњзуЁї![]() гыЁї
гыЁї![]() ЕФУцЛ§ЕФБШжЕЮЊ
ЕФУцЛ§ЕФБШжЕЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com