
科目:高中数学 来源:数学教研室 题型:013
下列命题中,正确的命题是
①三个平面把空间最多可以分成8部分.
②若直线a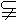 平面a
,直线b
平面a
,直线b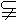 平面b
,则“a与b相交”与“a与b
相交”可以互推.
平面b
,则“a与b相交”与“a与b
相交”可以互推.
③若平面a
∩平面b
=直线l,a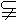 a
,b
a
,b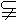 b
,且a∩b=点P,则PÎ
l.
b
,且a∩b=点P,则PÎ
l.
④若n条直线中任意两条共面,则它们共面.
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:013
①三个平面把空间最多可以分成8部分;
②若直线a![]() 平面α,直线b
平面α,直线b![]() 平面β,则“a与b相交”与“α与β相交”可互推;
平面β,则“a与b相交”与“α与β相交”可互推;
③若平面α∩平面β=直线l,a![]() α,b
α,b![]() β,且a∩b=点P,则P∈l;
β,且a∩b=点P,则P∈l;
④若n条直线中任意两条共面,则它们共面.
A.①与② B.②与③ C.③与④ D.①与③
查看答案和解析>>
科目:高中数学 来源: 题型:013
下列命题中,正确的命题是
①三个平面把空间最多可以分成
8部分.②若直线
a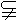 平面a
,直线b
平面a
,直线b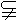 平面b
,则“a与b相交”与“a与b
相交”可以互推.
平面b
,则“a与b相交”与“a与b
相交”可以互推.
③若平面a ∩平面b
=直线l,a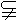 a
,b
a
,b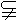 b
,且a∩b=点P,则PÎ
l.
b
,且a∩b=点P,则PÎ
l.
④若
n条直线中任意两条共面,则它们共面.[
]|
A .①② |
B .②③ |
C .③④ |
D .①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:
①三个平面把空间最多可以分成8部分;
②若直线a![]() 平面α,直线b
平面α,直线b![]() 平面β,则“a与b相交”与“α与β相交”可互推;
平面β,则“a与b相交”与“α与β相交”可互推;
③若平面α∩平面β=直线l,a![]() α,b
α,b![]() β,且a∩b=点P,则P∈l;
β,且a∩b=点P,则P∈l;
④若n条直线中任意两条共面,则它们共面.
A.①与② B.②与③ C.③与④ D.①与③
查看答案和解析>>
科目:高中数学 来源: 题型:
①三个平面把空间最多可以分成8部分;
②若直线a![]() 平面α,直线b
平面α,直线b![]() 平面β,则“a与b相交”与“α与β相交”可互推;
平面β,则“a与b相交”与“α与β相交”可互推;
③若平面α∩平面β=直线l,a![]() α,b
α,b![]() β,且a∩b=点P,则P∈l;
β,且a∩b=点P,则P∈l;
④若n条直线中任意两条共面,则它们共面.
A.①与② B.②与③ C.③与④ D.①与③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com