
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C 与y 轴交于A,B 两点,且|AB|=2.
,椭圆C 与y 轴交于A,B 两点,且|AB|=2.
(Ⅰ)求椭圆C 的方程;
(Ⅱ)设点P是椭圆C上的一个动点,且点P在y轴的右侧.直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆与x 轴交于两点E,F,求点P横坐标的取值范围及|EF|的最大值.
【答案】解:(Ⅰ)由题意可得,2b=2,即b=1, ![]() ,得
,得 ![]() ,
,
解得a2=4,
椭圆C的标准方程为 ![]() ;
;
(Ⅱ)方法一、设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),
所以 ![]() ,直线PA的方程为
,直线PA的方程为 ![]() ,
,
同理:直线PB的方程为 ![]() ,
,
直线PA与直线x=4的交点为 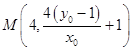 ,
,
直线PB与直线x=4的交点为 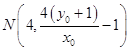 ,
,
线段MN的中点 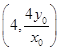 ,
,
所以圆的方程为 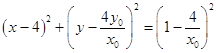 ,
,
令y=0,则 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,
,
设交点坐标(x1 , 0),(x2 , 0),可得x1=4+  ,x2=4﹣
,x2=4﹣  ,
,
因为这个圆与x轴相交,该方程有两个不同的实数解,
所以 ![]() ,解得
,解得 ![]() .
.
则 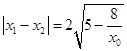 (
( ![]() )
)
所以当x0=2时,该圆被x轴截得的弦长为最大值为2.
方法二:设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),
所以 ![]() ,直线PA的方程为
,直线PA的方程为 ![]() ,
,
同理:直线PB的方程为 ![]() ,
,
直线PA与直线x=4的交点为 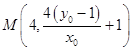 ,
,
直线PB与直线x=4的交点为 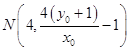 ,
,
若以MN为直径的圆与x轴相交,
则 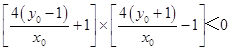 ,
,
即 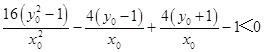 ,
,
即 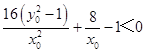 .
.
因为 ![]() ,所以
,所以 ![]() ,
,
代入得到 ![]() ,解得
,解得 ![]() .
.
该圆的直径为 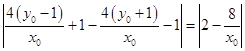 ,
,
圆心到x轴的距离为 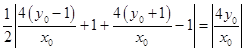 ,
,
该圆在x轴上截得的弦长为 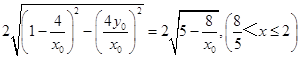 ;
;
所以该圆被x轴截得的弦长为最大值为2.
方法三:设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),
所以 ![]() ,直线PA的方程为
,直线PA的方程为 ![]() ,
,
同理:直线PB的方程为 ![]() ,
,
直线PA与直线x=4的交点为 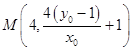 ,
,
直线PB与直线x=4的交点为 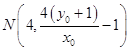 ,
,
所以 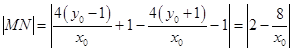 ,
,
圆心到x轴的距离为 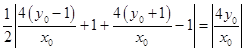 ,
,
若该圆与x轴相交,则 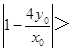
![]() ,
,
即 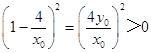 ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,解得
,解得 ![]() ,
,
该圆在x轴上截得的弦长为 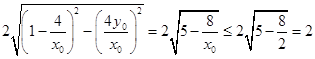 ;
;
所以该圆被x轴截得的弦长为最大值为2
【解析】(Ⅰ)由题意可得,2b=2,再由椭圆的离心率公式和a,b,c的关系,解得a=2,进而得到椭圆方程;(Ⅱ)方法一、设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),求出直线PA,PB的方程,与直线x=4的交点M,N,可得MN的中点,圆的方程,令y=0,求得与x轴的交点坐标,运用弦长公式,结合 ![]() .即可得到所求最大值;
.即可得到所求最大值;
方法二、设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),求出直线PA,PB的方程,与直线x=4的交点M,N,以MN为直径的圆与x轴相交,可得yMyN<0,求得 ![]() ,再由弦长公式,可得最大值;
,再由弦长公式,可得最大值;
方法三、设P(x0 , y0)(0<x0≤2),A(0,1),B(0,﹣1),求出直线PA,PB的方程,与直线x=4的交点M,N,可得MN的长度,由直线和圆相交,可得 ![]() ,再由弦长公式,可得最大值.
,再由弦长公式,可得最大值.


科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表如下所示:
优秀 | 非优秀 | 总计 | |
A班 | 14 | 6 | 20 |
B班 | 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
则下列说法正确的是 ( )
A. 有99%的把握认为环保知识测试成绩与专业有关
B. 有99%的把握认为环保知识测试成绩与专业无关
C. 有95%的把握认为环保知识测试成绩与专业有关
D. 有95%的把握认为环保知识测试成绩与专业无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求圆![]() 和直线l的极坐标方程;
和直线l的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线l与圆
,直线l与圆![]() 相交于A,B,求
相交于A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+ ![]() )(ω>0)的最小正周期为π,则该函数的图象( )
)(ω>0)的最小正周期为π,则该函数的图象( )
A.关于直线x= ![]() 对称
对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求圆C的直角坐标方程(化为标准方程)和直线l的极坐标方程;
(2)若直线l与圆C只有一个公共点,且a<1,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com