
分析 由题意画出图形,以BC边所在直线为x轴,以BC的垂直平分线为y轴建立平面直角坐标系,求出D、B、C、A的坐标,设出E的坐标,由已知列式求得E的坐标,进一步求出$\overrightarrow{DE}$的坐标,代入向量模的公式得答案.
解答 解:如图,以BC边所在直线为x轴,以BC的垂直平分线为y轴建立平面直角坐标系,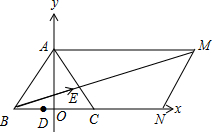
则D(-$\frac{1}{2}$,0),B($-\frac{3}{2}$,0),C($\frac{3}{2},0$),A(0,$\frac{3\sqrt{3}}{2}$),
设E(x,y),
则由2$\overrightarrow{BC}$+$\overrightarrow{BA}$=3$\overrightarrow{BE}$,得(6,0)+($\frac{3}{2},\frac{3\sqrt{3}}{2}$)=($\frac{9}{2}+3x$,3y),
即$\left\{\begin{array}{l}{\frac{15}{2}=\frac{9}{2}+3x}\\{\frac{3\sqrt{3}}{2}=3y}\end{array}\right.$,解得E(1,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{DE}=(\frac{3}{2},\frac{\sqrt{3}}{2})$,则$|\overrightarrow{DE}|=\sqrt{(\frac{3}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}=\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查平面向量的数量积运算,正确建立平面直角坐标系是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
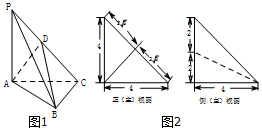 如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知a,b,m∈R,命题“若am2<bm2,则a<b”为假命题 | |
| B. | “x>3”是“x>2”的必要不充分条件 | |
| C. | 命题“p或q”为真命题,¬p为真,则命题q为假命题 | |
| D. | 命题“?x0∈R,x02-x0>0”的否定是:“?x∈R,x2-x≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7个 | B. | 3个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
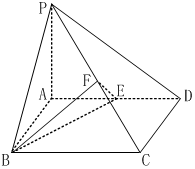 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2$\sqrt{2}$,E,F分别是AD,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2$\sqrt{2}$,E,F分别是AD,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com