
已知: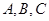 是
是 的内角,
的内角,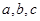 分别是其对边长,向量
分别是其对边长,向量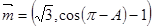 ,
, ,
,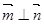 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若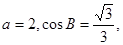 求
求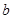 的长.
的长.
(Ⅰ)  . (Ⅱ)
. (Ⅱ)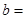
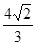 。
。
【解析】
试题分析:(I)根据 .可得
.可得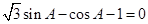 ,进一步转化可得
,进一步转化可得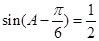 ,
,
从而可求出A值.
(II)再(I)的基础上可知在三角形ABC中,已知角A,B,边a,从而可利用正弦定理求b.
(Ⅰ)  =
=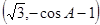 ……1分
……1分
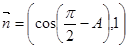 =
=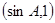 ……2分
……2分
∵
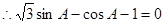 ……4分
……4分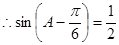 ……6分
……6分
∵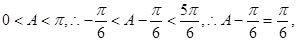 ……7分
……7分 .……8分
.……8分
(Ⅱ)在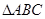 中,
中,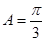 ,
,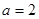 ,
,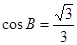
 ……9分由正弦定理知:
……9分由正弦定理知: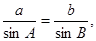 ……10分
……10分

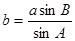 =
=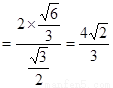 .
.
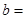
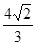 ……12分
……12分
考点:向量的数量积的坐标表示,两角差的正弦公式,给值求角,正弦定理.
点评:掌握向量的数量积的坐标表示是解决此问题的突破口,再利用两角差的正弦公式可求得A角,然后还要知道正弦定理可解决两类三角形问题:一是已知两边及一边的对角,二是知道两角及一边.


科目:高中数学 来源:2010年浙江省高一下学期期中考试数学(1-4班) 题型:解答题
已知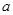 、
、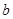 、
、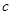 分别是
分别是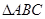 的三个内角
的三个内角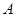 、
、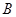 、
、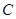 所对的边,
所对的边,
(Ⅰ)若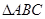 面积
面积 求
求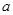 、
、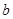 的值;
的值;
(Ⅱ)若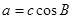 ,且
,且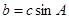 ,试判断
,试判断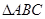 的形状.
的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com