
【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取![]() 名进行了问卷调查,得到
名进行了问卷调查,得到![]() 列联表,从这
列联表,从这![]() 名同学中随机抽取
名同学中随机抽取![]() 人,抽到“收看奥运会足球赛 ”的学生的概率是
人,抽到“收看奥运会足球赛 ”的学生的概率是![]() .
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
(1)请将上面的![]() 列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
(2)若从这![]() 名同学中的男同学中随机抽取
名同学中的男同学中随机抽取![]() 人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为
人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
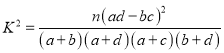 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,第五组
,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
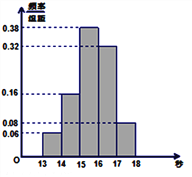
(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
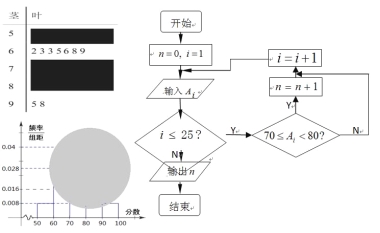
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com