
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:

(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(ⅰ)求抽取的文科生和理科生的人数;
(ⅱ)从10人的样本中随机抽取两人,求两人都是文科生的概率.
参考数据:

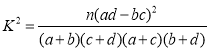 ,
,![]() .
.
【答案】(1)列联表见解析,没有;(2)(ⅰ)3人,7人;(ⅱ)![]() .
.
【解析】
(1)通过调查结果表可以知道:理科生中不太了解有28人,比较了解有42人,共计70人,文科生中不太了解有18人,比较了解有12人,共计30人,这样可以完成列联表的填写,再根据![]() 的计算公式求出
的计算公式求出![]() ,然后根据所给的数据做出解答;
,然后根据所给的数据做出解答;
(2)(ⅰ)根据理科生与文科生的人数之比,可以求出抽取的文科生和理科生的人数;
(ⅱ)记“两人都是文科生”为事件![]() ,记样本中的3名文科生为
,记样本中的3名文科生为![]() ,7名理科生为
,7名理科生为![]() ,从10人的样本中随机抽取两人,用列举法列出基本事件,然后求出
,从10人的样本中随机抽取两人,用列举法列出基本事件,然后求出![]() .
.
(1)依题意填写列联表如下:
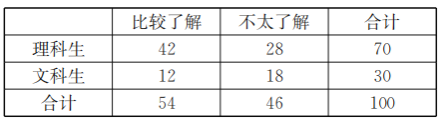
计算![]() ,
,
∴没有99%的把握认为,了解阿基米德与选择文理科有关
(2)(ⅰ)抽取的文科生人数是![]() (人),理科生人数是
(人),理科生人数是![]() (人).
(人).
(ⅱ)记“两人都是文科生”为事件![]() ,记样本中的3名文科生为
,记样本中的3名文科生为![]() ,7名理科生为
,7名理科生为![]() ,从10人的样本中随机抽取两人,则所有的基本事件有:
,从10人的样本中随机抽取两人,则所有的基本事件有:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
共45种,
两人都是文科生的基本事件有:![]() ,共3种,
,共3种,
故由古典概型得,两人都是文科生的概率是![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
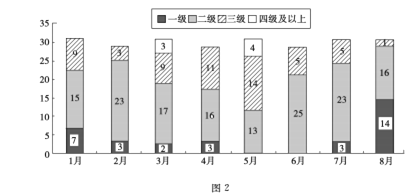
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图,在直二面角![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,且
,且![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() (不包含端点)上是否存在点
(不包含端点)上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,写出
;若存在,写出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于(参考公式:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线 y=ex在切线y=x+1的上方,故有不等式ex≥x+1.类比上述推理:对于函数y=lnx(x>0),有不等式( )
A. lnx≥x+1(x>0)B. lnx≤1﹣x(x>0)
C. lnx≥x﹣1(x>0)D. lnx≤x﹣1(x>0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com