练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知定义在R上的函数f（x）的图象关于原点对称，当x＞0时，有f（x）=2x-log3（x2-3x+5），则f（-2）=-3．

    分析 由题意，定义在R上的函数f（x）的图象关于原点对称，可知函数是奇函数，求出当x＜0时的解析式，可得答案．

    解答 解：由题意，定义在R上的函数f（x）的图象关于原点对称，可知函数是奇函数，f（-x）=-f（x）．
    当x＞0时，有f（x）=2x-log3（x2-3x+5），
    当x＜0时，则-x＞0，有f（-x）=2-x-log3（x2+3x+5）=-f（x）．
    ∴当x＜0时，有f（x）=-2-x+log3（x2+3x+5），
    则f（-2）=-22+log3（22-3×2+5）=-4+1=-3
    故答案为：-3．

    点评 本题考查了函数解析式的求法即带值计算问题，利用函数是奇函数这性质．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．设集合S={0，1，2，3，…，n}，则集合S中任意两个元素的差的绝对值的和为$\frac{1}{6}$n3+$\frac{1}{2}$n2+$\frac{1}{3}$n．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列判断错误的是（　　）
    A．“am2＜bm2”是“a＜b”的充分不必要条件
    B．命题“?x∈R，x2-x-1≤0”的否定是“$?{x_0}∈{R}，{x_0}^2-{x_0}-1＞0$”
    C．若p，q均为假命题，则p∧q为假命题
    D．若ζ～B（4，0.25），则Dξ=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．过点（1，2）且与直线2x+y-10=0垂直的直线方程是x-2y+3=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．求值：（1）（-1.8）0+（$\frac{2}{3}$）-2•（3$\frac{3}{8}$）${\;}^{\frac{2}{3}}$-$\frac{1}{\sqrt{0.01}}$+$\sqrt{{9}^{3}}$
    （2）lg500+lg$\frac{8}{5}$-$\frac{1}{2}$lg64+50（lg2+lg5）2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+x，x≤1}\\{lo{g}_{0.5}x，x＞1}\end{array}\right.$若对于任意x∈R，不等式f（x）≤$\frac{{t}^{2}}{4}$-t+1恒成立，则实数t的取值范围是（-∞，1]∪[3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，焦距为2c，直线$y=\frac{{\sqrt{3}}}{3}（x+c）$与双曲线的一个交点P满足∠PF2F1=2∠PF1F2，则双曲线的离心率e为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．$2\sqrt{3}+1$D．$\sqrt{3}+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．一直线l过直线l1：3x-y=3和直线l2：x-2y=2的交点P，且与直线l3：x-y+1=0垂直．
    （1）求直线l的方程；
    （2）若直线l与圆心在x正半轴上的半径为$\sqrt{2}$的圆C相切，求圆C的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

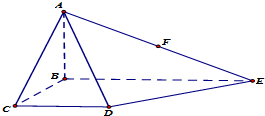    3．如图，在四棱锥A-BCDE中，底面BCDE是∠BCD=90°的梯形，CD∥BE，AB⊥底面BCDE，BE=4AB=2BC=2CD，点F为AE的中点．
    （1）求证：FD∥平面ABC；
    （2）求异面直线AC与DE所成角的余弦值．

    查看答案和解析>>

    同步练习册答案