
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,且
的中点,且![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离 .
的距离 .
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)要证线面垂直,一般先证线线垂直,一个在![]() 中,利用勾股定理证得
中,利用勾股定理证得![]() ,然后由于三棱柱的侧棱与底面垂直,从而侧面与底面垂直,而底面是等腰直角三角形,
,然后由于三棱柱的侧棱与底面垂直,从而侧面与底面垂直,而底面是等腰直角三角形, ![]() 与
与![]() 垂直,从而
垂直,从而![]() 与侧面
与侧面![]() 垂直,于是有
垂直,于是有![]() ,由线面垂直的判定定理可得;
,由线面垂直的判定定理可得;
(Ⅱ)要求![]() 点到平面
点到平面![]() 的距离,在四面体
的距离,在四面体![]() 中
中![]() 的面积易求,可把此四面体看作以
的面积易求,可把此四面体看作以![]() 为顶点,以
为顶点,以![]() 为底面的三棱锥,这时棱锥的高与底面积易求,从而由体积法可求得题设距离.
为底面的三棱锥,这时棱锥的高与底面积易求,从而由体积法可求得题设距离.
试题解析:
(Ⅰ)证明:连接![]() .
.
∵![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边
斜边![]() 的中点,所以
的中点,所以![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)解:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,∴
,∴![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
, ![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,解得
,解得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若函数y=f(x)同时满足:(ⅰ)对于定义域内的任意x,恒有f(x)+f(﹣x)=0;(ⅱ)对于定义域内的任意x1 , x2 , 当x1≠x2时,恒有![]() , 则称函数f(x)为“二维函数”.现给出下列四个函数:
, 则称函数f(x)为“二维函数”.现给出下列四个函数:
①f(x)=![]()
②f(x)=﹣x3+x
③![]()
④![]()
其中能被称为“二维函数”的有 (写出所有满足条件的函数的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.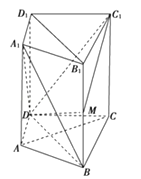
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() ,
, ![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() ,
, ![]() 的斜率分别是
的斜率分别是![]() ,
, ![]() ,满足
,满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
(1)求A和f(x)的值域C;
(2)若A∩B=[2,3],求实数m的值;
(3)若CRB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过20万元时,按销售利润的20%进行奖励;当销售利润超过20万元时,若超出部分为A万元,则超出部分按2log5(A+2)进行奖励,没超出部分仍按销售利润的20%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员奖励方案的函数表达式;
(2)如果业务员老张获得8万元的奖励,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)频率分布直方图.

(1)已知该校大一学生有2400人,求抽取的100名学生中大一学生人数;
(2)根据频率分布直方图求该校大学生每周使用共享单车的平均时间.
(3)![]() 从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com