
【题目】已知数列{an}中,a1=3,n(an+1﹣an)=an+1,n∈N*若对于任意的a∈[﹣1,1],n∈N* , 不等式 ![]() ﹣2at+1恒成立,则实数t的取值范围是 .
﹣2at+1恒成立,则实数t的取值范围是 .
【答案】(﹣∞,﹣3]∪[3,+∞)
【解析】解:∵n(an+1﹣an)=an+1,
∴ ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() .
.
∴ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() +a1
+a1
= ![]() +
+ ![]() +…+
+…+ ![]() +3
+3
=1﹣ ![]() +3(n=1时也成立).
+3(n=1时也成立).
∴不等式 ![]() ﹣2at+1化为:4﹣
﹣2at+1化为:4﹣ ![]() <t2﹣2at+1,
<t2﹣2at+1,
∵对于任意的a∈[﹣1,1],n∈N*,不等式 ![]() ﹣2at+1恒成立,
﹣2at+1恒成立,
∴t2﹣2at+1≥4,
化为:t2﹣2at﹣3≥0,
t≠0,t>0时,a≤ ![]() ,可得1≤
,可得1≤ ![]() ,化为t2﹣2t﹣3≥0,t>0,解得t≥3.
,化为t2﹣2t﹣3≥0,t>0,解得t≥3.
t<0时,a≥ ![]() ,可得﹣1≥
,可得﹣1≥ ![]() ,化为t2+2t﹣3≥0,t<0,解得t≤﹣3.
,化为t2+2t﹣3≥0,t<0,解得t≤﹣3.
则实数t的取值范围是(﹣∞,﹣3]∪[3,+∞).
故答案为:(﹣∞,﹣3]∪[3,+∞).
n(an+1﹣an)=an+1,化为: ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() .利用
.利用 ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() +a1
+a1
可得 ![]() ,不等式
,不等式 ![]() ﹣2at+1化为:4﹣
﹣2at+1化为:4﹣ ![]() <t2﹣2at+1,根据对于任意的a∈[﹣1,1],n∈N*,不等式
<t2﹣2at+1,根据对于任意的a∈[﹣1,1],n∈N*,不等式 ![]() ﹣2at+1恒成立,可得t2﹣2at+1≥4,化为:t2﹣2at﹣3≥0,对t分类讨论即可得出.
﹣2at+1恒成立,可得t2﹣2at+1≥4,化为:t2﹣2at﹣3≥0,对t分类讨论即可得出.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设M=10a2+81a+207,P=a+2,Q=26﹣2a,若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项. (Ⅰ)求a的值及{an}的通项公式;
(Ⅱ)记函数 ![]() 的图像在x轴上截得的线段长为bn , 设
的图像在x轴上截得的线段长为bn , 设 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为 . 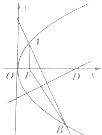
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an>0,n=1,2,…,且a5a2n﹣5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n﹣1=( )
A.n(2n﹣1)
B.(n+1)2
C.n2
D.(n﹣1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>5,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知t= ![]() (u>1),且关于t的不等式t2﹣8t+m+18<0有解,则实数m的取值范围是( )
(u>1),且关于t的不等式t2﹣8t+m+18<0有解,则实数m的取值范围是( )
A.(﹣∞,﹣3)
B.(﹣3,+∞)
C.(3,+∞)
D.(﹣∞,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的等差数列{an}前n项和为Sn , 首项a1=3,数列{bn} 为等比数列,首项b1=1,且b2S2=64,b3S3=960.
(1)求an和bn;
(2)设f(n)= ![]() (n∈N*),求f(n)最大值及相应的n的值.
(n∈N*),求f(n)最大值及相应的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 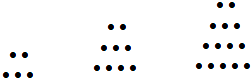
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com