
����Ŀ��ij���˹�˾��A��B�����ͺŵij����е��ס������ؼ�ij�;����ҵ��ÿ��ÿ������һ�Σ�A��B���ֳ������ؿ����ֱ�Ϊ36�˺�60�ˣ��Ӽ�ȥ�ҵص�Ӫ�˳ɱ��ֱ�Ϊ1600Ԫ/����2400Ԫ/������˾���齨һ��������21�����Ŀ��˳��ӣ���Ҫ��B�ͳ�������A�ͳ�7������ÿ��Ҫ�Բ�����900������Ӽ�ȥ�ҵص��ÿͣ���ʹ��˾�Ӽ�ȥ�ҵص�Ӫ�˳ɱ���С����ôӦ�䱸A�ͳ���B�ͳ�����������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������12����ijʳƷ��Ϊ�˼��һ���Զ���װ��ˮ�ߵ���������������ȡ����ˮ����![]() ����Ʒ��Ϊ�����Ƴ����ǵ���������λ�������������ķ�������Ϊ
����Ʒ��Ϊ�����Ƴ����ǵ���������λ�������������ķ�������Ϊ![]() ��
��![]() �� ��
�� ��![]() ���ɴ˵õ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
���ɴ˵õ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
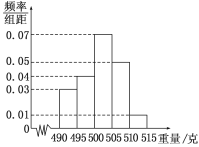
��1������Ƶ�ʷֲ�ֱ��ͼ������������![]() �˵IJ�Ʒ������
�˵IJ�Ʒ������
��2����������ȡ��![]() ����Ʒ����ȡ
����Ʒ����ȡ![]() ������
������![]() ��������
Ϊ��������![]() �˵IJ�Ʒ��������
�˵IJ�Ʒ��������![]() �ķֲ��У�
�ķֲ��У�
��3���Ӹ���ˮ������ȡ![]() ����Ʒ����ǡ��
����Ʒ����ǡ��![]() ����Ʒ����������
����Ʒ����������![]() �˵ĸ��ʣ�
�˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ס������������羥Ҷͼ��ʾ�������ǵ���λ����ͬ��ƽ����Ҳ��ͬ�� 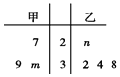
��1����m��n��ȡֵ��
��2���Ƚϼס����������ݵ��ȶ��ԣ���˵�����ɣ�
ע�����ʽs2= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABC��A1B1C1�У���BAC=90�㣬AB=AC=AA1=1���ӳ�A1C1����P��ʹC1P=A1C1 �� ����AP����CC1�ڵ�D����A1Ϊ����ԭ�㽨���ռ�ֱ������ϵ����ͼ��ʾ��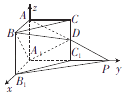
��1��д��A1��B��B1��C��D��P�����ꣻ
��2��������ֱ��A1B��PB1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}����a1+3a2+32a3+��+3n��1an= ![]() ��n��N* ��
��n��N* ��
��1��������{an}��ͨ�
��2���� ![]() ��������{bn}��ǰn���Sn ��
��������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪԲO��ֱ������E��F��ԲO�ϣ�AB��EF������ABCD���ڵ�ƽ����ԲO���ڵ�ƽ�滥�ഹֱ����֪AB=2��EF=1��
������֤��ƽ��DAF��ƽ��CBF��
������ֱ��AB��ƽ��CBF���ɽǵĴ�С��
����AD�ij�Ϊ��ֵʱ��ƽ��DFC��ƽ��FCB���ɵ������ǵĴ�СΪ60�㣿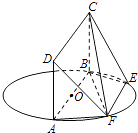
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ǵ�λԲ�ϵ����㣬A��B����ֱ��ڵ�һ�������ޣ���C��Բ��x��������Ľ��㣬�ǡ�AOB= ![]() ������A������Ϊ��
������A�������� ![]() ��
�� ![]() �����ǡ�COA=����
�����ǡ�COA=���� 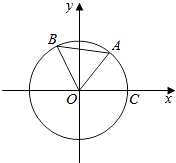
��1���� ![]() ��ֵ��
��ֵ��
��2�����B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}�У�a1=��2������d=3������{bn}�У�SnΪ��ǰn��ͣ����㣺2nSn+1=2n��n��N+��
����An= ![]() ��������An��ǰn���S��
��������An��ǰn���S��
������֤������{bn}�ǵȱ����У�
����������{cn}����cn=anbn �� TnΪ����{cn}��ǰn�����������{xn}����x1=c2��c1 �� ��xn= ![]() ��������{xn}�����ֵ��
��������{xn}�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���2x2��bx+ ![]() =0������Ϊsin�ȡ�cos�ȣ��ȡʣ�
=0������Ϊsin�ȡ�cos�ȣ��ȡʣ� ![]() ��
�� ![]() ����
����
��1����ʵ��b��ֵ��
��2���� ![]() +
+ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com