某产品生产单位产品时的总成本函数为.每单位产品的价格是134元.求使利润最大时的产量. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

（本小题满分12分）某产品生产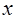单位产品时的总成本函数为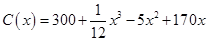.每单位产品的价格是134元，求使利润最大时的产量.

工厂生产36单位产品时有最大利润996元.

解析

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

依法纳税是每个公民应尽的义务，国家征收个人工资、薪金所得税是分段计算的：总收入不超过2 000元的，免征个人工资、薪金所得税；超过2 000元部分需征税，设全月纳税所得额(所得额指工资、薪金中应纳税的部分)为x，x＝全月总收入－2 000元，税率如表所示：

级数	全月应纳税所得额x	税率
1	不超过500元部分	5%
2	超过500元至2 000元部分	10%
3	超过2 000元至5 000元部分	15%
…	…	…
9	超过100 000元部分	45%

(1)若应纳税额为f(x)，试用分段函数表示1～3级纳税额f(x)的计算公式；
(2)某人2008年10月份工资总收入为4 200元，试计算这个人10月份应纳个人所得税多少元？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

沪杭高速公路全长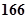千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于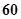千米/时且不高于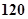千米/时的时速匀速行驶到杭州.已知该汽车每小时的运输成本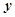(以元为单位)由可变部分和固定部分组成：可变部分与速度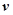(千米/时)的平方成正比，比例系数为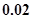；固定部分为200元.
(1)把全程运输成本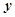(元)表示为速度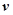(千米/时)的函数，并指出这个函数的定义域；
(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

已知函数的图象是曲线C，直线与曲线
C相切于点（1，3）.
（1）求函数的解析式；
（2）求函数的递增区间；
（3）求函数上的最大值和最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元. 根据市场调查，销售商一次订购量不会超过500件。
(1)设一次订购量为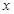件，服装的实际出厂单价为元，写出函数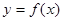的表达式；
(2)当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？
（服装厂售出一件服装的利润=实际出厂单价－成本）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

有一边长为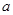的正方形铁片，铁片的四角截去四个边长为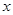的小正方形，然后做成一个无盖方盒。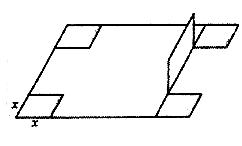

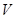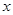（1）试把方盒的容积表示成的函数；
（2）求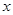多大时，做成方盒的容积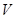最大。

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算，如果将楼房建为x(≥10)层，则每平方米的平均建筑费用为560+48（单位：元）.为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝）