
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在①中,(0,+∞)是f(x)=|x|的唯一可等域区间;在②中,[-1,1]是唯一的可等域区间;在③中,函数只有一个等可域区间[0,1]; 在④中,函数无可等域区间.
解答 解:在①中,(0,+∞)是f(x)=|x|的唯一可等域区间,故①成立;
在②中,f(x)=2x2-1≥-1,且f(x)在x≤0时递减,在x≥0时递增,
若0∈[m,n],则-1∈[m,n],于是m=-1,又f(-1)=1,f(0)=-1,而f(1)=1,故n=1,
[-1,1]是一个可等域区间;
若n≤0,则{2n2−1=m2m2−1=n,解得m=−1−√54,n=−1+√54>0,不合题意,
若m≥0,则2x2-1=x有两个非负解,但此方程的两解为1和-12,也不合题意,
故函数f(x)=2x2-1只有一个等可域区间[-1,1],故②成立;
在③中,函数f(x)=|1-2x|的值域是[0,+∞),所以m≥0,
函数f(x)=|1-2x|在[0,+∞)上是增函数,考察方程2x-1=x,
由于函数y=2x与y=x+1只有两个交点(0,1),(1,2),即方程2x-1=x只有两个解0和1,
因此此函数只有一个等可域区间[0,1],故③成立;
在④中,函数f(x)=log2(2x-2)在定义域(1,+∞)上是增函数,
若函数有f(x)=log2(2x-2)等可域区间[m,n],则f(m)=m,f(n)=n,
但方程log2(2x-2)=x无解(方程x=log2x无解),故此函数无可等域区间,故④不成立.
综上只有①②③正确.
故选:C.
点评 本题考查函数的可等域区间的判断,是中档题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
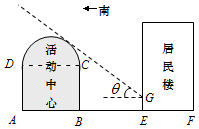 如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足tanθ=34.
如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足tanθ=34.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com